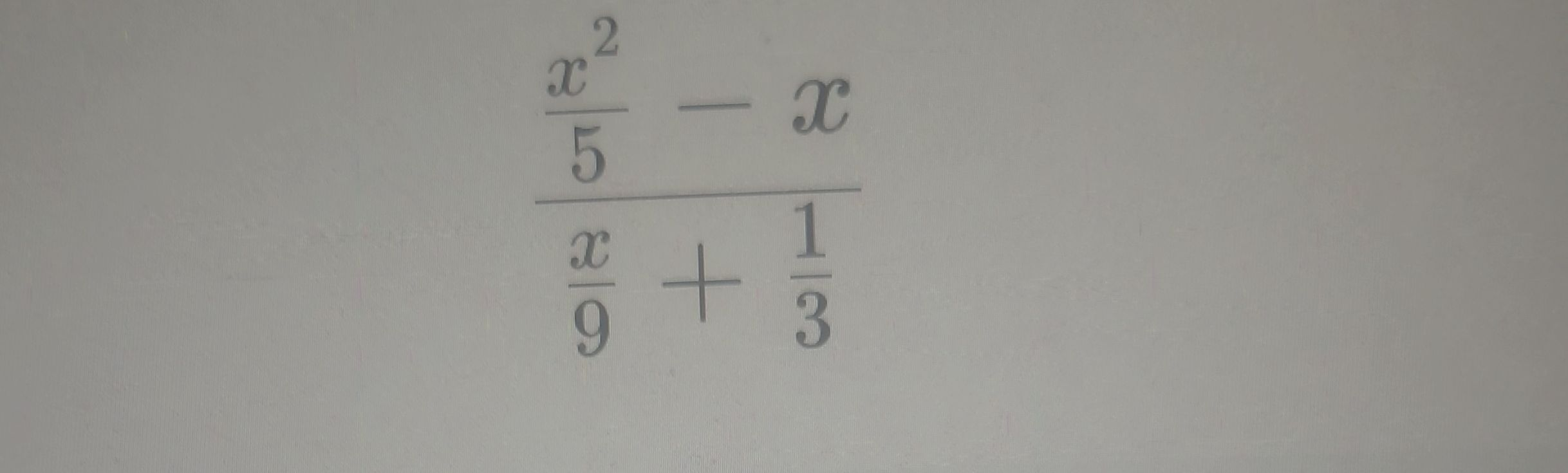((x^(2))/(5)-x)/((x)/(9)+(1)/(3))

Question

Bytelearn · Accepted Answer

Identify Given Expression: Identify the given expression and look for common denominators in the numerator and the denominator to combine terms. The expression is ((x^(2))/(5)-x)/((x)/(9)+(1)/(3)).Combine Common Denominators: Combine the terms in the denominator by finding a common denominator. The common denominator for (x/9) and (1/3) is 9. So, (x/9) + (1/3) becomes (x/9) + (3/9) which simplifies to (x+3)/9.Rewrite with Simplified Denominator: Rewrite the expression with the simplified denominator. The expression now is ((x^(2))/(5)-x)/((x+3)/9).Multiply by Least Common Multiple: To simplify the complex fraction, multiply the numerator and the denominator by the least common multiple (LCM) of the denominators inside the complex fraction, which is 45. So, we multiply ((x^(2))/(5)-x) and ((x+3)/9) by 45/45.Multiply Numerator by 45: Multiply the terms in the numerator by 45. (x^(2)/5)*45 = 9x^2 and -x*45 = -45x. So, the numerator becomes 9x^2 - 45x.Multiply Denominator by 45: Multiply the terms in the denominator by 45. (x+3)/9*45 = 5(x+3). So, the denominator becomes 5(x+3).Rewrite with Multiplied Numerator/Denominator: Rewrite the expression with the multiplied numerator and denominator. The expression now is (9x^2 - 45x)/(5(x+3)).Factor Out Common Factor: Factor out the common factor in the numerator. The common factor is 9x, so factor it out to get 9x(x - 5). The expression now is 9x(x - 5)/(5(x+3)).Check for Common Factors: Check for any common factors that can be canceled out from the numerator and the denominator. There are no common factors to cancel out between 9x(x - 5) and 5(x+3).

$\frac{\frac{x^{2}}{5}-x}{\frac{x}{9}+\frac{1}{3}}$

Full solution

More problems from Operations with rational exponents

Related topics

x25−xx9+13 \frac{\frac{x^{2}}{5}-x}{\frac{x}{9}+\frac{1}{3}} 9x​+31​5x2​−x​

$\frac{\frac{x^{2}}{5}-x}{\frac{x}{9}+\frac{1}{3}}$