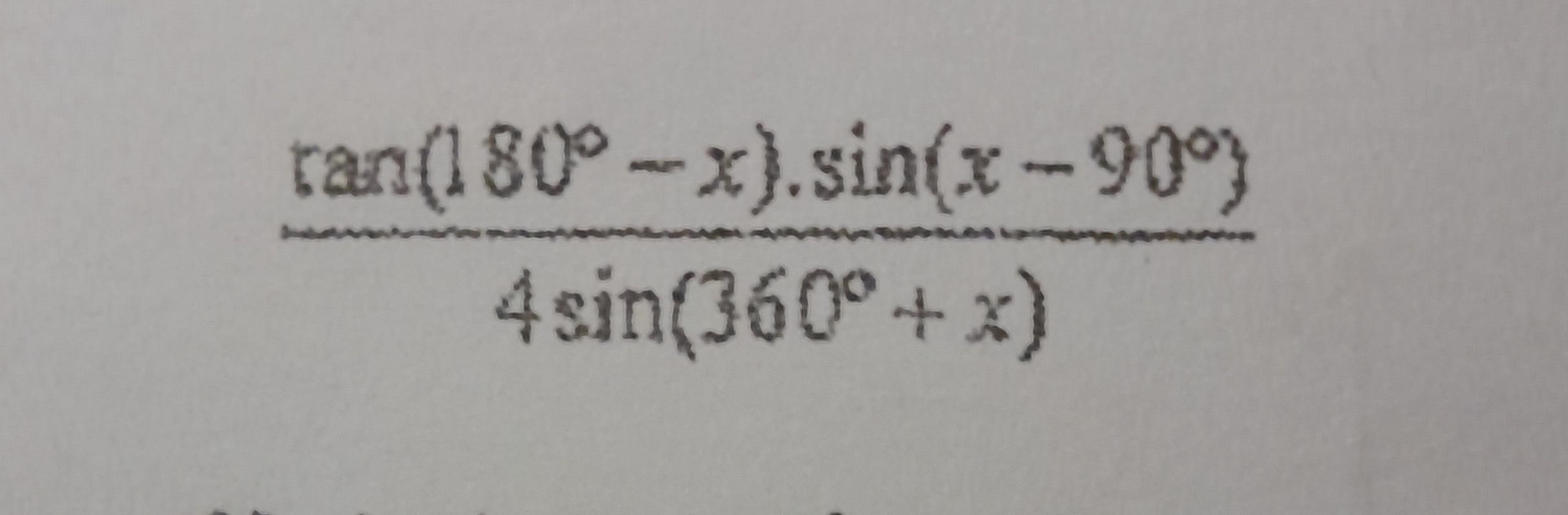Solve. (tan(180^(@)-x)*sin(x-90^(@)))/(4sin(360^(@)+x))

Question

Bytelearn · Accepted Answer

Use Trigonometric Identities: We will use trigonometric identities to simplify the expression. The first identity we will use is the tangent subtraction formula: tan(180°-x) = -tan(x). This is because tangent is negative in the second quadrant, and 180° puts us in the second quadrant. Calculation: tan(180°-x) = -tan(x)Simplify sin(x-90°): Next, we will simplify sin(x-90°). The sine function has a period of 360°, so subtracting 90° shifts the phase by 90° counterclockwise. This is equivalent to the cosine function, but since we are in the second quadrant, it will be negative: sin(x-90°) = -cos(x). Calculation: sin(x-90°) = -cos(x)Simplify sin(360°+x): Now, we will simplify sin(360°+x). Since sine has a period of 360°, adding 360° to the angle does not change the value of the sine function: sin(360°+x) = sin(x). Calculation: sin(360°+x) = sin(x)Substitute Simplified Expressions: We can now substitute the simplified trigonometric expressions back into the original expression: (tan(180°-x)*sin(x-90°))/(4sin(360°+x)) = (-tan(x)*(-cos(x)))/(4sin(x)). Calculation: Substitute the simplified expressions.Cancel Negative Signs: We notice that there are negative signs in both the numerator and the denominator, which will cancel each other out: (-tan(x)*(-cos(x)))/(4sin(x)) = (tan(x)*cos(x))/(4sin(x)). Calculation: Cancel out the negative signs.Use tan(x) Identity: We can simplify further by using the identity tan(x) = sin(x)/cos(x). Substituting this into our expression gives us: (tan(x)*cos(x))/(4sin(x)) = (sin(x)/cos(x)*cos(x))/(4sin(x)). Calculation: Substitute tan(x) with sin(x)/cos(x).Cancel cos(x): The cos(x) in the numerator and the cos(x) in the denominator cancel each other out, leaving us with: (sin(x)/cos(x)*cos(x))/(4sin(x)) = sin(x)/(4sin(x)). Calculation: Cancel out cos(x).Simplify Final Expression: Finally, we can simplify sin(x)/(4sin(x)) by canceling out sin(x) in the numerator and the denominator: sin(x)/(4sin(x)) = 1/4. Calculation: Cancel out sin(x).

Solve. $\newline$ $\frac{\tan \left(180^{\circ}-x\right) \cdot \sin \left(x-90^{\circ}\right)}{4 \sin \left(360^{\circ}+x\right)}$

Full solution

More problems from Operations with rational exponents

Related topics

Solve.\newlinetan⁡(180∘−x)⋅sin⁡(x−90∘)4sin⁡(360∘+x) \frac{\tan \left(180^{\circ}-x\right) \cdot \sin \left(x-90^{\circ}\right)}{4 \sin \left(360^{\circ}+x\right)} 4sin(360∘+x)tan(180∘−x)⋅sin(x−90∘)​

Solve. $\newline$ $\frac{\tan \left(180^{\circ}-x\right) \cdot \sin \left(x-90^{\circ}\right)}{4 \sin \left(360^{\circ}+x\right)}$