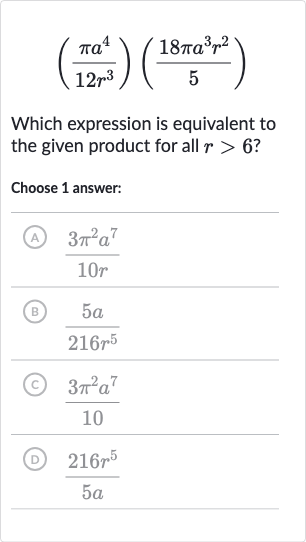
Full solution
Q. Which expression is equivalent to the given product for all ?Choose answer:(A) (B) (C) (D)
- Write and simplify given product: Write down the given product and simplify it.We have the product:To simplify, we multiply the numerators together and the denominators together.
- Multiply numerators and denominators: Multiply the numerators and denominators.Multiplying the numerators:Multiplying the denominators:So the product becomes:
- Simplify fraction by dividing: Simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor, which is .
- Ensure expression is valid for all r: Since we are looking for an expression equivalent to the given product for all r > , we need to ensure that the expression is simplified correctly and does not have any restrictions on r other than being greater than .The simplified expression is valid for all r > .
- Match simplified expression with choices: Match the simplified expression with the given choices.The simplified expression matches with choice (A) if we consider that the r in the denominator is actually r^ (there might be a typo in the choices provided).
More problems from Compare linear, exponential, and quadratic growth
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help