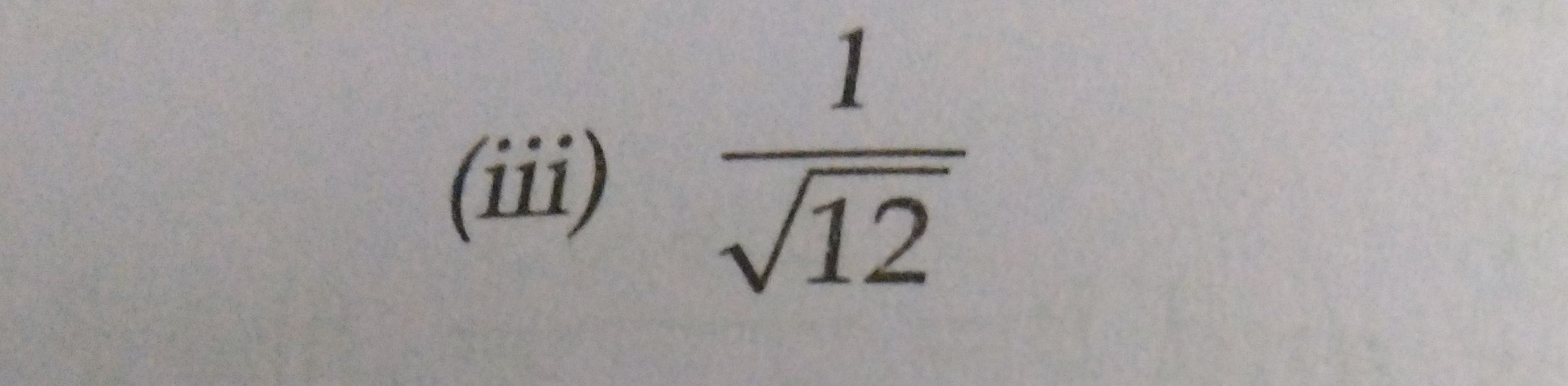AI tutor
Full solution
Q. (iii)
- Recognize Simplification: Simplify the expression .First, recognize that can be simplified because is not a prime number and has square factors.
- Factorize : Factor into its prime factors to find squares that can be taken out of the square root..
- Rewrite Square Root: Rewrite using the prime factorization..
- Take Out Square Root: Take the square root of the perfect square out of the square root..
- Divide by Simplified Root: Now, simplify the original expression by dividing by ..
- Rationalize Denominator: To rationalize the denominator, multiply the numerator and the denominator by ..
- Simplify Denominator: Simplify the denominator..
- Final Simplification: The expression is now fully simplified..
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help