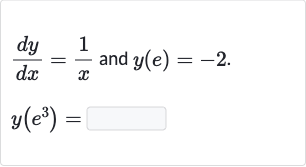Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(dy)/(dx)=(1)/(x) and
y(e)=-2.

y(e^(3))=

$\frac{d y}{d x}=\frac{1}{x}$ and $y(e)=-2$ . $\newline$ $y\left(e^{3}\right)=$

View step-by-step help

View step-by-step help

Csc, sec, and cot of special angles

Full solution

Q.

\frac{d y}{d x}=\frac{1}{x}

and

y(e)=-2

.

\newline

y\left(e^{3}\right)=

Integrate and solve equation: Integrate both sides of the equation $\frac{dy}{dx}=\frac{1}{x}$ to find $y(x)$ . $\int dy = \int \frac{1}{x} dx$ $y = \ln|x| + C$
Find constant using initial condition: Substitute $x=e$ to find the constant $C$ using the initial condition $y(e)=-2$ . $\newline$ $-2 = \ln|e| + C$ $\newline$ $-2 = 1 + C$ $\newline$ $C = -3$
Write general solution: Write the general solution for $y(x)$ with the found constant $C$ . $\newline$ $y(x) = \ln|x| - 3$
Substitute $x=e^3$ : Substitute $x=e^{3}$ into the general solution to find $y(e^{3})$ .
$y(e^{3}) = \ln|e^{3}| - 3$
$y(e^{3}) = 3\ln|e| - 3$
Simplify expression: Simplify the expression since $\ln|e|=1$ . $\newline$ $y(e^{3}) = 3(1) - 3$ $\newline$ $y(e^{3}) = 3 - 3$
Calculate final value: Calculate the final value of $y(e^{3})$ . $y(e^{3}) = 0$

More problems from Csc, sec, and cot of special angles

Question

Marco's class is painting a mural on the side of their school. The mural covers a

3 \frac{1}{2} \mathrm{~m}

high, rectangular wall. It has an area of

28 \mathrm{~m}^{2}

\newline

What is the length of the mural?

\newline

Posted 3 months ago

Question

A cup of hot coffee has been left to cool in a room with an ambient temperature of

21^{\circ} \mathrm{C}

\newline

The relationship between the elapsed time,

m

, in minutes, since the coffee was left to cool, and the temperature of the coffee,

T

{ }^{\circ} \mathrm{C}

, is modeled by the following function.

\newline

T(m)=21+74 \cdot 10^{-0.03 m}

\newline

What will the temperature of the coffee be after

10

\newline

Round your answer, if necessary, to the nearest hundredth.

\newline

{ }^{\circ} C

Posted 3 months ago

Question

Takumi plants a tree in his backyard and studies how the number of branches grows over time.

\newline

He predicts that the relationship between

N

, the number of branches on the tree, and

t

, the elapsed time, in years, since the tree was planted can be modeled by the following equation.

\newline

N=5 \cdot 10^{0.3 t}

\newline

According to Takumi's model, in how many years will the tree have

100

\newline

Give an exact answer expressed as a base

-10

\newline

Posted 3 months ago

Question

g(x)=2^{x}

\newline

Can we use the mean value theorem to say the equation

g^{\prime}(x)=16

has a solution where

3<x<5

\newline

1

\newline

(A) No, since the function is not differentiable on that interval.

\newline

(B) No, since the average rate of change of

g

over the interval

3 \leq x \leq 5

1 \overline{6}

\newline

(C) Yes, both conditions for using the mean value theorem have been met.

Posted 3 months ago

Question

\frac{d}{d x}\left(\frac{x^{2}-x+5}{4 x-1}\right)=

Posted 3 months ago

Question

\frac{d}{d x}\left(\frac{2 x^{2}+x-3}{2 x+7}\right)=

Posted 3 months ago

Question

\frac{d}{d x}\left(\frac{3 x^{2}-1}{x-2}\right)=

Posted 3 months ago

Question

\frac{d y}{d t}=2 t+3 \text { and } y(1)=6

\newline

t

y=0

\newline

Choose all answers that apply:

\newline

t=-1

\newline

t=-3

\newline

t=0

\newline

t=-4

\newline

t=1

\newline

t=-2

Posted 3 months ago

Question

\frac{d}{d x}\left(x^{\frac{3}{4}}\right)=

Posted 3 months ago

Question

y=x^{13}

\newline

\frac{d y}{d x}=

Posted 3 months ago