Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(((a)/(b)))/(c)*(a)/(((b)/(c)))
Which of the following is equivalent to the given expression?
Choose 1 answer:
(A)
(a^(2))/(b^(2))
(B)
(a^(2))/(c^(2))
(C)
(a^(2))/(b^(2)c^(2))
(D)
(a^(2)c^(2))/(b^(2))

$\frac{\left(\frac{a}{b}\right)}{c} \cdot \frac{a}{\left(\frac{b}{c}\right)}$ $\newline$ Which of the following is equivalent to the given expression? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{a^{2}}{b^{2}}$ $\newline$ (B) $\frac{a^{2}}{c^{2}}$ $\newline$ (c) $\frac{a^{2}}{b^{2} c^{2}}$ $\newline$ (D) $\frac{a^{2} c^{2}}{b^{2}}$

View step-by-step help

View step-by-step help

Compare linear and exponential growth

Full solution

Q.

\frac{\left(\frac{a}{b}\right)}{c} \cdot \frac{a}{\left(\frac{b}{c}\right)}

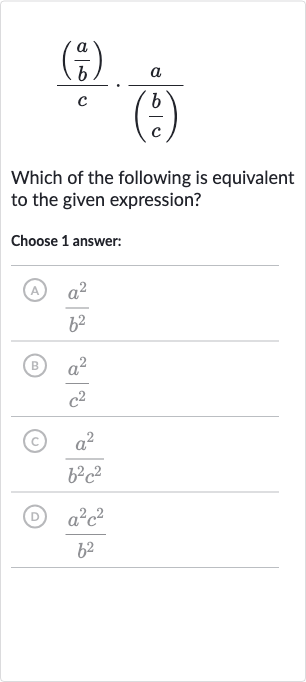
\newline

Which of the following is equivalent to the given expression?

\newline

Choose

1

answer:

\newline

(A)

\frac{a^{2}}{b^{2}}

\newline

(B)

\frac{a^{2}}{c^{2}}

\newline

(c)

\frac{a^{2}}{b^{2} c^{2}}

\newline

(D)

\frac{a^{2} c^{2}}{b^{2}}

Multiply by reciprocal: Simplify the given expression by multiplying the numerator and denominator by the reciprocal of the denominator. $\newline$ The given expression is: $\left(\frac{a}{b}\right)\bigg/\left(\frac{c}{a}\right)\cdot\frac{a}{\left(\frac{b}{c}\right)}$ $\newline$ We can rewrite this as: $\left(\frac{a}{b}\right) \cdot \left(\frac{1}{c}\right) \cdot a \cdot \left(\frac{c}{b}\right)$
Cancel out common factors: Simplify the expression by canceling out common factors. $\newline$ The $c$ in the numerator and the $c$ in the denominator cancel each other out, as do the $b$ in the numerator and the $b$ in the denominator. $\newline$ This leaves us with: $\frac{a \cdot a}{b \cdot b}$
Use exponents: Rewrite the simplified expression using exponents. $\newline$ The expression $(a \cdot a) / (b \cdot b)$ can be written as: $(a^2) / (b^2)$
Match with answer choices: Match the simplified expression with the given answer choices. $\newline$ The expression $(a^2) / (b^2)$ corresponds to answer choice (A).

More problems from Compare linear and exponential growth

Question

Jill bought a used motorcycle from a seller online for $1,200. The seller will charge her $5 a day to store the motorcycle at his house until she is able to pick it up. You can use a function to describe the total amount of money Jill will owe the seller if she waits

x

days to pick up the motorcycle.

\newline

Write an equation for the function. If it is linear, write it in the form

g(x) = mx + b

. If it is exponential, write it in the form

g(x) = a(b)^x

\newline

g(x) = \underline{\hspace{3em}}

Posted 5 months ago

Question

f(t)=-2t-7

change over the interval from

t=-7

t=-6

\newline

\newline

\left[\text{f(t) decreases by } 2\right]

\newline

\left[\text{f(t) increases by } 2\right]

\newline

\left[\text{f(t) increases by } 200\%\right]

\newline

\left[\text{f(t) decreases by a factor of } 2\right]

Posted 5 months ago

Question

g(t)=9^t

change over the interval from

t=1

t=3

\newline

\newline

\left[\text{g(t) decreases by a factor of } 81\right]

\newline

\left[\text{g(t) increases by a factor of } 81\right]

\newline

\left[\text{g(t) increases by } 18\%\right]

\newline

\left[\text{g(t) decreases by } 9\%\right]

Posted 5 months ago

Question

Both of these functions grow as

x

gets larger and larger. Which function eventually exceeds the other?

\newline

\newline

(A)f(x) = 8x + 3.3

\newline

(B)g(x) = 3.3^x - 5

Posted 6 months ago

Question

Both of these functions grow as

x

gets larger and larger. Which function eventually exceeds the other?

\newline

\newline

(A) \ f(x) = 2x + 9

\newline

(B)\ g(x) = 2^x

Posted 6 months ago

Question

f(x)

g(x)

are differentiable.

\newline

h(x)

h(x)=\frac{g(x)}{f(x)}

\newline

f(8)=1

f'(8)=-6

g(8)=8

g'(8)=-10

h'(8)

\newline

Simplify any fractions.

\newline

h'(8)=

Posted 6 months ago

Question

p(x)

q(x)

are differentiable.

\newline

r(x)

r(x)= \frac{p(x)}{q(x)}

\newline

p(3)= 2

p'(3)= 4

q(3)= 6

q'(3)= 9

r'(3)

\newline

Simplify any fractions.

\newline

r'(3)=

Posted 7 months ago

Question

u(x)

v(x)

are differentiable.

\newline

w(x)

w(x)= \frac{u(x)}{v(x)}

\newline

u(5)= 3

u'(5)= -2

v(5)= 7

v'(5)= 1

w'(5)

\newline

Simplify any fractions.

\newline

w'(5)=

Posted 7 months ago

Question

a(x)

b(x)

are differentiable.

\newline

c(x)

c(x)= \frac{a(x)}{b(x)}

\newline

a(2)= 4

a'(2)= 5

b(2)= 1

b'(2)= -3

c'(2)

\newline

Simplify any fractions.

\newline

c'(2)=

Posted 7 months ago

Question

m(x)

n(x)

are differentiable.

\newline

o(x)

o(x)= \frac{m(x)}{n(x)}

\newline

m(7)= 2

m'(7)= -1

n(7)= 4

n'(7)= 8

o'(7)

\newline

Simplify any fractions.

\newline

o'(7)=

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant