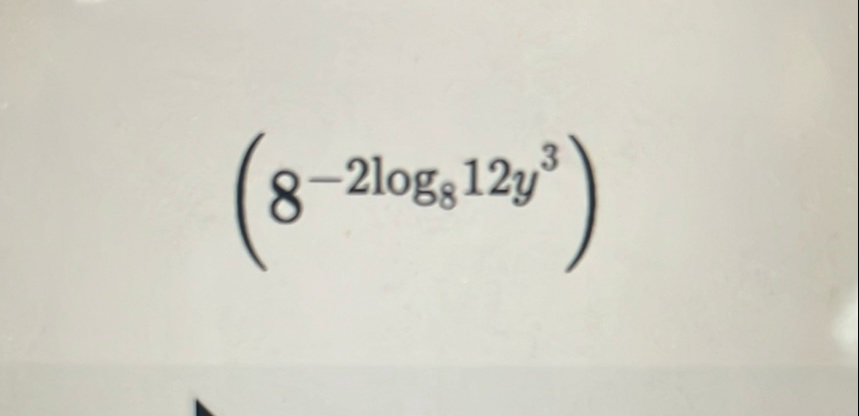(8^(-2log_(8)12y^(3)))

Question

Bytelearn · Accepted Answer

Identify base and exponent: Identify the base of the logarithm and the exponent. The base of the logarithm is 8, and the exponent is -2 times the logarithm of 12y^3 to the base 8.Apply power rule: Use the power rule of logarithms which states that log_b(a^c) = c * log_b(a). In this case, we have log base 8 of (12y^3), which can be written as 3 * log base 8 of 12y.Apply power rule to exponent: Apply the power rule to the exponent of 8. The expression -2log_(8)12y^(3) becomes -2 * 3 * log_(8)12y = -6log_(8)12y.Rewrite using property of exponents: Rewrite the expression using the property of exponents that states a^(m*n) = (a^m)^n. In this case, 8^(-6log_(8)12y) can be written as (8^(-6))^log_(8)12y.Simplify base: Simplify 8^(-6). Since 8 is 2^3, we can write 8^(-6) as (2^3)^(-6), which simplifies to 2^(-18).Apply change of base formula: Apply the change of base formula for logarithms. The expression log_(8)12y can be written as log(12y)/log(8), where log denotes the common logarithm (base 10).Simplify expression: Simplify the expression (2^(-18))^log(12y)/log(8). Since the base is now 2, we can use the property of exponents that states (a^b)^c = a^(b*c). This gives us 2^(-18 * log(12y)/log(8)).Recognize final form: Recognize that the expression 2^(-18 * log(12y)/log(8)) is the final simplified form of the original expression. There is no further simplification possible without knowing the value of y.

$\left(8^{-2 \log _{8} 12 y^{3}}\right)$

Full solution

More problems from Evaluate rational exponents

Related topics

(8−2log⁡812y3) \left(8^{-2 \log _{8} 12 y^{3}}\right) (8−2log8​12y3)

$\left(8^{-2 \log _{8} 12 y^{3}}\right)$