Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(3g^(2)+12 g)/(g+7)*(4)/(8g^(2))
Which expression is equivalent to the product for all
g > 0 ?
Choose 1 answer:
(A)
(3g+48)/(g^(2)+56 g)
(B)
(12 g+12)/(8g^(2)+7g)
(c)
(3g+12)/(2g^(2)+14 g)
(D)
(3+12 g)/(2g+14)

$\frac{3 g^{2}+12 g}{g+7} \cdot \frac{4}{8 g^{2}}$ $\newline$ Which expression is equivalent to the product for all g>0 ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{3 g+48}{g^{2}+56 g}$ $\newline$ (B) $\frac{12 g+12}{8 g^{2}+7 g}$ $\newline$ (C) $\frac{3 g+12}{2 g^{2}+14 g}$ $\newline$ (D) $\frac{3+12 g}{2 g+14}$

View step-by-step help

View step-by-step help

Compare linear and exponential growth

Full solution

Q.

\frac{3 g^{2}+12 g}{g+7} \cdot \frac{4}{8 g^{2}}

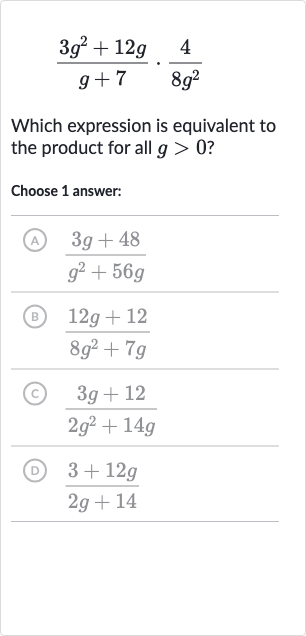
\newline

Which expression is equivalent to the product for all

g>0

?

\newline

Choose

1

answer:

\newline

(A)

\frac{3 g+48}{g^{2}+56 g}

\newline

(B)

\frac{12 g+12}{8 g^{2}+7 g}

\newline

(C)

\frac{3 g+12}{2 g^{2}+14 g}

\newline

(D)

\frac{3+12 g}{2 g+14}

Factor Common Factor: First, let's factor out the common factor in the numerator of the first fraction. $\newline$ $3g^2 + 12g$ can be factored as $3g(g + 4)$ . $\newline$ So, the expression becomes $(3g(g + 4))/(g + 7) \times (4)/(8g^2)$ .
Simplify Second Fraction: Next, we simplify the second fraction by dividing both the numerator and the denominator by $4$ . $\newline$ $(4)/(8g^2)$ simplifies to $(1)/(2g^2)$ . $\newline$ Now, the expression is $(3g(g + 4))/(g + 7) \times (1)/(2g^2)$ .
Multiply Fractions: We can now multiply the two fractions together. $\newline$ When multiplying fractions, we multiply the numerators together and the denominators together. $\newline$ $(3g(g + 4))/(g + 7) \times (1)/(2g^2)$ becomes $(3g(g + 4))/(2g^2(g + 7))$ .
Cancel Simplify: We can simplify the expression by canceling out a $g$ from the numerator and the $g^2$ in the denominator. $\newline$ This leaves us with $(3(g + 4))/(2g(g + 7))$ .
Distribute Numerator Denominator: Now, we distribute the $3$ in the numerator and the $2g$ in the denominator. $\newline$ This gives us $(3g + 12)/(2g^2 + 14g)$ .
Check Answer Choices: We check the answer choices to see which one matches our simplified expression. $\newline$ The correct answer is (C) $(3g + 12)/(2g^2 + 14g)$ .

More problems from Compare linear and exponential growth

Question

Jill bought a used motorcycle from a seller online for $1,200. The seller will charge her $5 a day to store the motorcycle at his house until she is able to pick it up. You can use a function to describe the total amount of money Jill will owe the seller if she waits

x

days to pick up the motorcycle.

\newline

Write an equation for the function. If it is linear, write it in the form

g(x) = mx + b

. If it is exponential, write it in the form

g(x) = a(b)^x

\newline

g(x) = \underline{\hspace{3em}}

Posted 5 months ago

Question

f(t)=-2t-7

change over the interval from

t=-7

t=-6

\newline

\newline

\left[\text{f(t) decreases by } 2\right]

\newline

\left[\text{f(t) increases by } 2\right]

\newline

\left[\text{f(t) increases by } 200\%\right]

\newline

\left[\text{f(t) decreases by a factor of } 2\right]

Posted 5 months ago

Question

g(t)=9^t

change over the interval from

t=1

t=3

\newline

\newline

\left[\text{g(t) decreases by a factor of } 81\right]

\newline

\left[\text{g(t) increases by a factor of } 81\right]

\newline

\left[\text{g(t) increases by } 18\%\right]

\newline

\left[\text{g(t) decreases by } 9\%\right]

Posted 5 months ago

Question

Both of these functions grow as

x

gets larger and larger. Which function eventually exceeds the other?

\newline

\newline

(A)f(x) = 8x + 3.3

\newline

(B)g(x) = 3.3^x - 5

Posted 6 months ago

Question

Both of these functions grow as

x

gets larger and larger. Which function eventually exceeds the other?

\newline

\newline

(A) \ f(x) = 2x + 9

\newline

(B)\ g(x) = 2^x

Posted 6 months ago

Question

f(x)

g(x)

are differentiable.

\newline

h(x)

h(x)=\frac{g(x)}{f(x)}

\newline

f(8)=1

f'(8)=-6

g(8)=8

g'(8)=-10

h'(8)

\newline

Simplify any fractions.

\newline

h'(8)=

Posted 6 months ago

Question

p(x)

q(x)

are differentiable.

\newline

r(x)

r(x)= \frac{p(x)}{q(x)}

\newline

p(3)= 2

p'(3)= 4

q(3)= 6

q'(3)= 9

r'(3)

\newline

Simplify any fractions.

\newline

r'(3)=

Posted 7 months ago

Question

u(x)

v(x)

are differentiable.

\newline

w(x)

w(x)= \frac{u(x)}{v(x)}

\newline

u(5)= 3

u'(5)= -2

v(5)= 7

v'(5)= 1

w'(5)

\newline

Simplify any fractions.

\newline

w'(5)=

Posted 7 months ago

Question

a(x)

b(x)

are differentiable.

\newline

c(x)

c(x)= \frac{a(x)}{b(x)}

\newline

a(2)= 4

a'(2)= 5

b(2)= 1

b'(2)= -3

c'(2)

\newline

Simplify any fractions.

\newline

c'(2)=

Posted 7 months ago

Question

m(x)

n(x)

are differentiable.

\newline

o(x)

o(x)= \frac{m(x)}{n(x)}

\newline

m(7)= 2

m'(7)= -1

n(7)= 4

n'(7)= 8

o'(7)

\newline

Simplify any fractions.

\newline

o'(7)=

Posted 7 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant