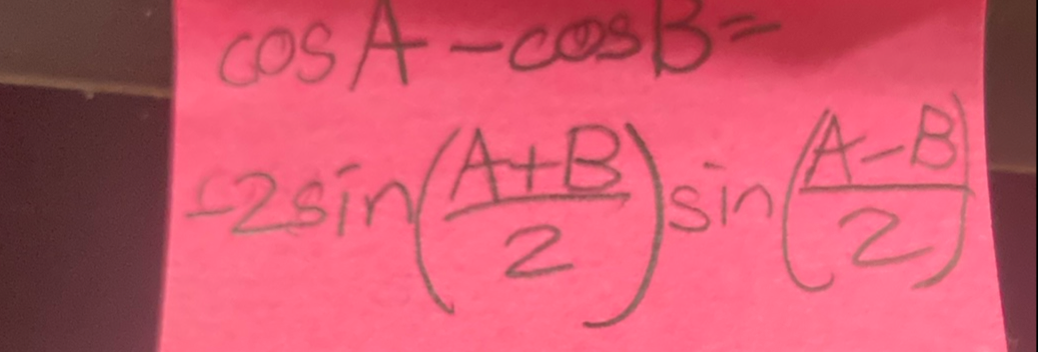AI tutor
Full solution
Q. Prove the trigonometric identity.
- Apply Sine Angle Subtraction Formula: Use the sine angle subtraction formula: . So, .
- Simplify Cosines: Simplify the cosines inside the brackets: , and .So, .
- Eliminate Negative Sign: Multiply through by to get rid of the negative sign: .
- Final Multiplication: Now multiply by : .
More problems from Operations with rational exponents
QuestionGet tutor help
QuestionGet tutor help