AI tutor
Full solution
Q.
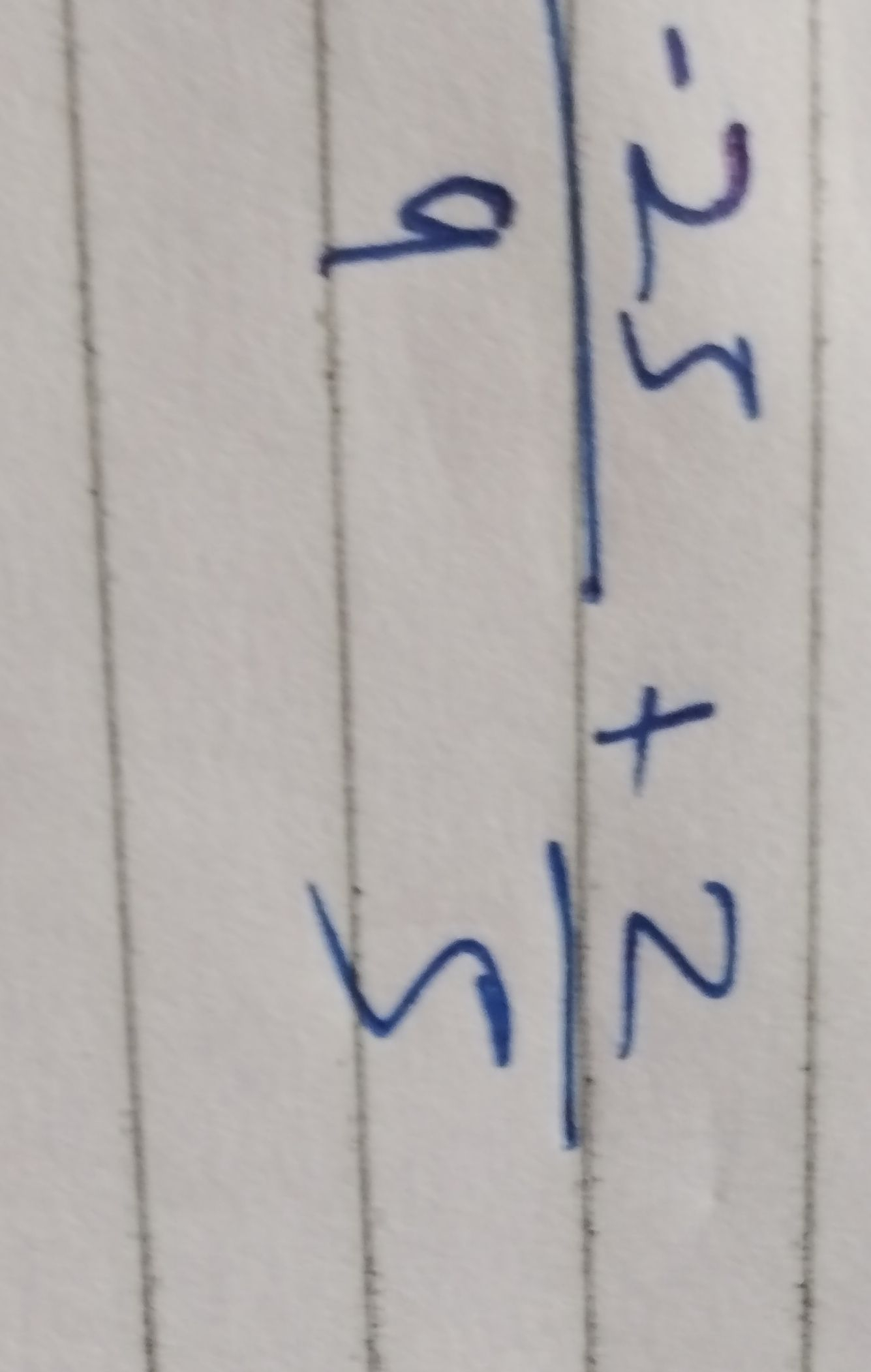
- Find Common Denominator: To add the fractions and , we need to find a common denominator. The least common multiple of and is .
- Convert to Equivalent Fractions: We convert each fraction to an equivalent fraction with a denominator of . For , we multiply the numerator and denominator by . For , we multiply the numerator and denominator by .
- Add Fractions: Now we can add the two fractions with the common denominator of . + = \)
- Perform Addition: We perform the addition in the numerator.
- Simplify Fraction: The sum of the two fractions is now a single fraction with the numerator and the denominator . is the simplified form of the sum, as the numerator and denominator have no common factors other than .
More problems from Evaluate rational exponents
QuestionGet tutor help
QuestionGet tutor help