AI tutor
Full solution
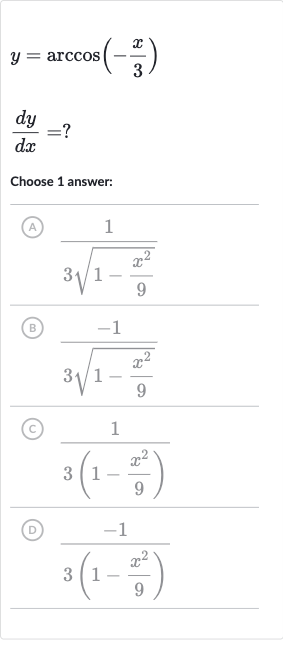
Q. Choose answer:(A) (B) (C) (D)
- Write Derivative of arccos(u): First, let's write down the derivative of with respect to , which is .
- Apply Chain Rule with : Now, we need to apply the chain rule. Let . The derivative of with respect to is .
- Calculate Derivative of y: So, the derivative of with respect to is the derivative of times the derivative of with respect to , which is .
- Substitute back in: Substitute back in to get .
- Simplify the Expression: Simplify the expression to get * .
- Final Result: The negatives cancel out, so we get .