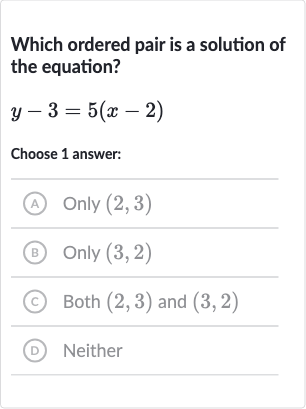
Full solution
Q. Which ordered pair is a solution of the equation?Choose answer:(A) Only (B) Only (C) Both and (D) Neither
- Check Solution : Step : Let's determine if the ordered pair satisfies the equation . Substituting and into the equation yields . Simplifying, we get , which simplifies to . This is true, so is a solution of the equation.
- Check Solution : Step : Now, let's check the second option . For this option, and . Substitute and into the equation . This gives us . Simplifying this, we get \-1=5(1), which simplifies to \-1=5. This is not true, so the ordered pair is not a solution of the equation.
- Final Answer: Step : Since the ordered pair is a solution and is not, the correct answer is Only .