Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

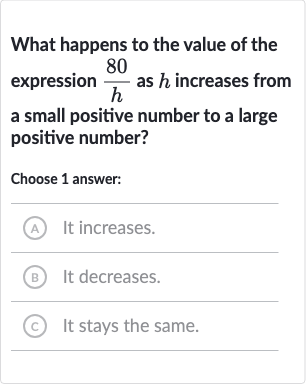
What happens to the value of the expression
(80 )/(h) as
h increases from a small positive number to a large positive number?
Choose 1 answer:
A It increases.
(B) It decreases.
(C) It stays the same.

What happens to the value of the expression $\frac{80}{h}$ as $h$ increases from a small positive number to a large positive number? $\newline$ Choose $1$ answer: $\newline$ (A) It increases. $\newline$ (B) It decreases. $\newline$ (C) It stays the same.

View step-by-step help

View step-by-step help

Slopes of parallel and perpendicular lines

Full solution

Q. What happens to the value of the expression

\frac{80}{h}

as

h

increases from a small positive number to a large positive number?

\newline

Choose

1

answer:

\newline

(A) It increases.

\newline

(B) It decreases.

\newline

(C) It stays the same.

Understanding the Relationship: Understand the relationship between the numerator and the denominator in the expression $(\frac{80}{h})$ . $\newline$ As $h$ increases, what happens to the fraction as a whole? $\newline$ Since $80$ is a constant and $h$ is in the denominator, as $h$ increases, the overall value of the fraction decreases.
Behavior as $h$ Approaches Infinity: Consider the behavior of the expression as $h$ approaches infinity. $\newline$ What is the limit of $\frac{80}{h}$ as $h$ approaches infinity? $\newline$ The limit of $\frac{80}{h}$ as $h$ approaches infinity is $0$ , which means the expression decreases towards $0$ as $h$ increases.
Correct Description of Behavior: Choose the correct answer based on the behavior of the expression. $\newline$ Which option correctly describes the behavior of $(80)/(h)$ as $h$ increases? $\newline$ Option (B) ＂It decreases＂ is the correct answer because as $h$ gets larger, the value of the expression gets smaller.

More problems from Slopes of parallel and perpendicular lines

Question

Convert the angle

\theta=260^{\circ}

\newline

Express your answer exactly.

\newline

\theta=\square \text { radians }

Posted 9 months ago

Question

Convert the angle

\theta=230^{\circ}

\newline

Express your answer exactly.

\newline

\theta=\square \text { radians }

Posted 9 months ago

Question

What happens to the value of the expression

1+3 f

f

\newline

1

\newline

(A) It increases.

\newline

(B) It decreases.

\newline

(C) It stays the same.

Posted 9 months ago

Question

-\frac{5}{4}+\frac{75}{40}+100 \%=

\newline

Enter the answer as an exact decimal or simplified fraction.

Posted 9 months ago

Question

-1 \frac{60}{100}+0.1+\frac{1}{4}=

\newline

Enter the answer as an exact decimal or simplified fraction.

Posted 9 months ago

Question

0.25-1.125-\frac{16}{8}=

\newline

Enter the answer as an exact decimal or simplified fraction.

Posted 9 months ago

Question

x^{3}+y^{2}=24

\newline

What is the value of

\frac{d^{2} y}{d x^{2}}

(2,4)

\newline

Give an exact number.

Posted 9 months ago

Question

Can this differential equation be solved using separation of variables?

\newline

\frac{d y}{d x}=x y+5 x

\newline

1

\newline

\newline

Posted 9 months ago

Question

g(x)=2(x-5)(x-3)

h(x)=2(x+5)(x+3)

are graphed in the

x y

-plane. Which of the following is a true statement?

\newline

1

\newline

(A) The functions have the same

y

\newline

(B) The functions have the same

x

\newline

(C) The functions have the same axis of symmetry.

\newline

(D) The functions have the same vertex.

Posted 9 months ago

Question

You pick a card at random, put it back, and then pick another card at random.

\newline

4

\newline

5

\newline

6

\newline

7

\newline

What is the probability of picking a number greater than

5

and then picking a

4

\newline

Write your answer as a percentage.

Posted 28 days ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant