Full solution
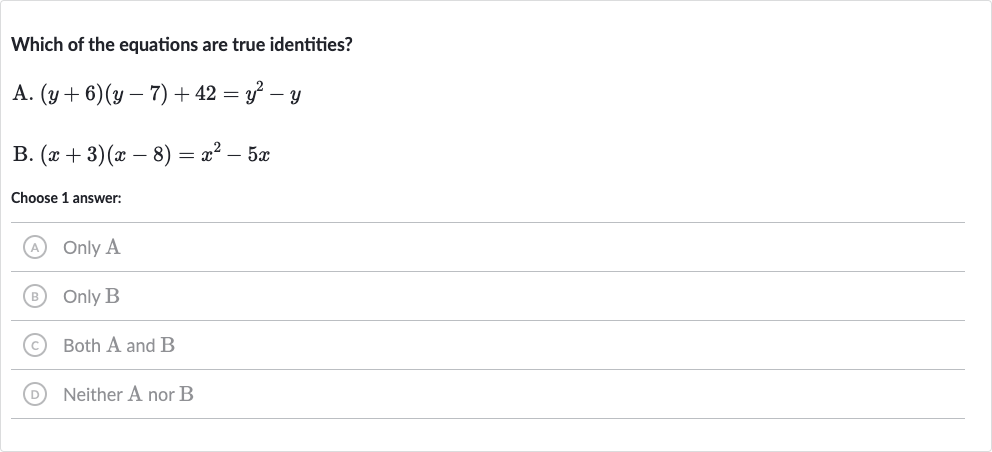
Q. Which of the equations are true identities?A. B. Choose answer:(A) Only A(B) Only B(C) Both A and B(D) Neither nor
- Expand Expression: Expand using the distributive property (FOIL method).
- Combine Like Terms: Combine like terms in the expansion.
- Add : Add to both sides of the equation from the original problem.
- Check Equation: Check if the left side of equation A is equal to the right side after simplification.
- Expand Expression: Expand using the distributive property (FOIL method).
- Combine Like Terms: Combine like terms in the expansion.