Full solution
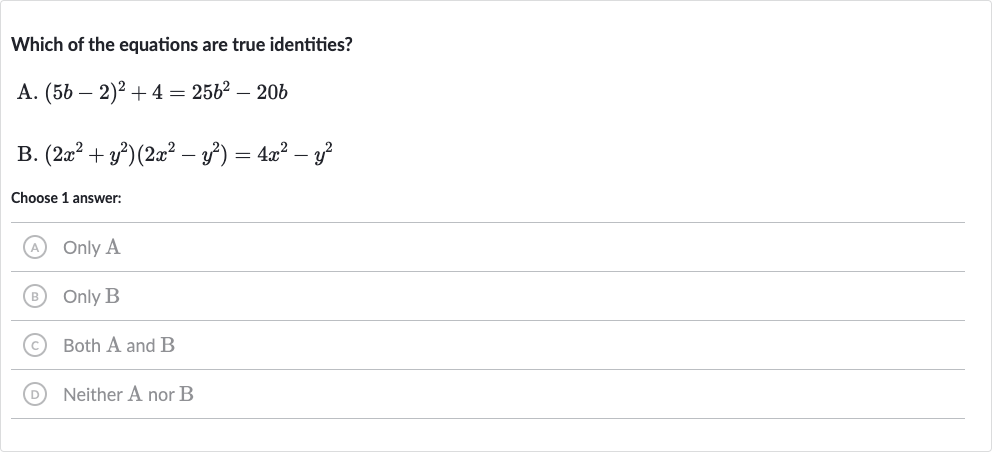
Q. Which of the equations are true identities?A. B. Choose answer:(A) Only A(B) Only B(C) Both A and B(D) Neither nor
- Expand : Expand in option A.
- Compare with option A: Compare the expanded form of with the right side of option A., which is not equal to .
- Option A evaluation: Option A is not a true identity because the left side does not equal the right side.
- Expand : Expand in option B using the difference of squares formula.
- Compare with option B: Compare the expanded form of with the right side of option B. is not equal to .