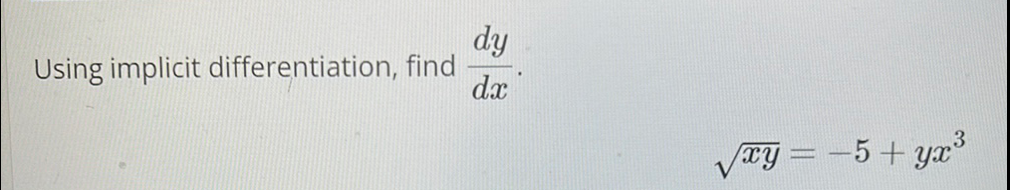Using implicit differentiation, find $\frac{d y}{d x}$ . $\newline$ $\sqrt{x y}=-5+y x^{3}$

View step-by-step help

Home

Math Problems

Calculus

Find derivatives using implicit differentiation

Full solution

Q. Using implicit differentiation, find

\frac{d y}{d x}

\newline

\sqrt{x y}=-5+y x^{3}

Apply Implicit Differentiation: First, we need to apply implicit differentiation to both sides of the equation with respect to $x$ . The equation is $\sqrt{xy} = -5 + yx^3$ . We will differentiate term by term.
Differentiate Left Side: Differentiate the left side, $\sqrt{xy}$ , with respect to $x$ . Using the chain rule, we get $\frac{1}{2}(xy)^{-\frac{1}{2}} \times (x\frac{dy}{dx} + y)$ .
Differentiate Right Side: Differentiate the right side, $-5 + yx^3$ , with respect to $x$ . The derivative of $-5$ is $0$ , and using the product rule for $yx^3$ , we get $3yx^2 + x^3\left(\frac{dy}{dx}\right)$ .
Equate Derivatives: Now we equate the derivatives from the left and right sides to get $(\frac{1}{2})(xy)^{-\frac{1}{2}} * (x\frac{dy}{dx} + y) = 3yx^2 + x^3\frac{dy}{dx}$ .
Solve for $\frac{dy}{dx}$ : We need to solve for $\frac{dy}{dx}$ . To do this, we'll collect all the terms containing $\frac{dy}{dx}$ on one side and the rest on the other side. This gives us $\frac{1}{2}(xy)^{-\frac{1}{2}} \cdot x\frac{dy}{dx} - x^3\frac{dy}{dx} = 3yx^2 - \frac{1}{2}(xy)^{-\frac{1}{2}} \cdot y$ .
Factor Out $(\frac{dy}{dx}):$ Factor out $(\frac{dy}{dx})$ from the terms on the left side to get (\frac{dy}{dx})((\frac{$1$}{$2$})(xy)^{-\frac{$1$}{$2$}} \cdot x - x^\(3) = $3$ yx^ $2$ - (\frac{ $1$ }{ $2$ })(xy)^{-\frac{ $1$ }{ $2$ }} \cdot y.
Isolate $(\frac{dy}{dx}):</b> Divide both sides by \$\left(\frac{1}{2}(xy)^{-\frac{1}{2}} \cdot x - x^3\right)$ to isolate $(\frac{dy}{dx})$ . This gives us (\frac{dy}{dx}) = \frac{$3$yx^$2$ - \left(\frac{$1$}{$2$}(xy)^{-\frac{$1$}{$2$}} \cdot y\right)}{\left(\frac{$1$}{$2$}(xy)^{-\frac{$1$}{$2$}} \cdot x - x^$3$\right)}.}
Simplify \((\frac{dy}{dx}): Simplify the expression for \$(\frac{dy}{dx}) if possible. However, in this case, the expression is already in its simplest form, so we have our final answer.

Using implicit differentiation, find dydx \frac{d y}{d x} dxdy​.\newlinexy=−5+yx3 \sqrt{x y}=-5+y x^{3} xy​=−5+yx3

Using implicit differentiation, find $\frac{d y}{d x}$ . $\newline$ $\sqrt{x y}=-5+y x^{3}$