Full solution
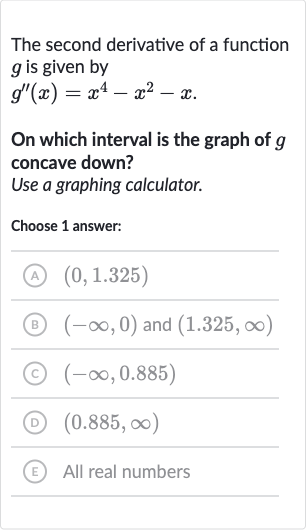
Q. The second derivative of a function is given byOn which interval is the graph of concave down?Use a graphing calculator.Choose answer:(A) (B) and (C) (D) (E) All real numbers
- Identify Concave Down: To find where the graph of is concave down, we need to find where its second derivative is less than .
- Calculate Second Derivative: . Set g''(x) < 0 and solve for .
- Use Graphing Calculator: We can't factor this easily, so we'll use a graphing calculator to find the intervals where is negative.
- Analyze Negative Intervals: After graphing , we see that the function is negative between two points, let's call them and .
- Determine Interval for Concavity: Using the graphing calculator, we find that the function changes from positive to negative at and from negative to positive at .
- Determine Interval for Concavity: Using the graphing calculator, we find that the function changes from positive to negative at and from negative to positive at .Therefore, the graph of is concave down on the interval .