Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

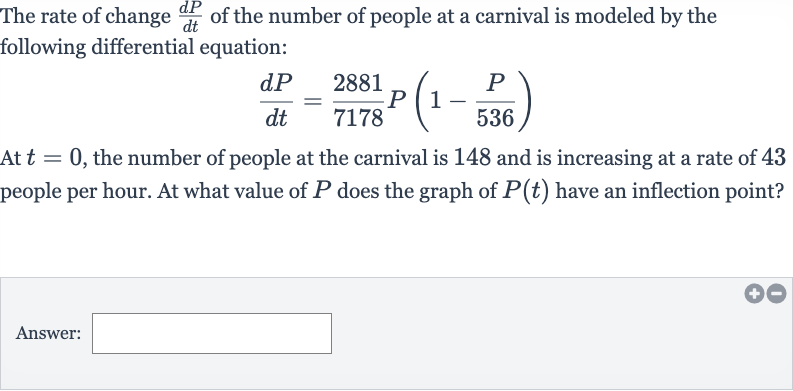
The rate of change
(dP)/(dt) of the number of people at a carnival is modeled by the following differential equation:

(dP)/(dt)=(2881)/(7178)P(1-(P)/( 536))
At
t=0, the number of people at the carnival is 148 and is increasing at a rate of 43 people per hour. At what value of
P does the graph of
P(t) have an inflection point?
Answer:

The rate of change $\frac{d P}{d t}$ of the number of people at a carnival is modeled by the following differential equation: $\newline$ $\frac{d P}{d t}=\frac{2881}{7178} P\left(1-\frac{P}{536}\right)$ $\newline$ At $t=0$ , the number of people at the carnival is $148$ and is increasing at a rate of $43$ people per hour. At what value of $P$ does the graph of $P(t)$ have an inflection point? $\newline$ Answer:

View step-by-step help

View step-by-step help

Find derivatives using logarithmic differentiation

Full solution

Q. The rate of change

\frac{d P}{d t}

of the number of people at a carnival is modeled by the following differential equation:

\newline

\frac{d P}{d t}=\frac{2881}{7178} P\left(1-\frac{P}{536}\right)

\newline

At

t=0

, the number of people at the carnival is

148

and is increasing at a rate of

43

people per hour. At what value of

P

does the graph of

P(t)

have an inflection point?

\newline

Answer:

Find Second Derivative: To find the inflection point, we need to find the second derivative of $P$ with respect to $t$ and then determine when it changes sign. The given differential equation is: $\newline$ $\frac{dP}{dt} = \frac{2881}{7178}P\left(1 - \frac{P}{536}\right)$ $\newline$ First, we need to find the first derivative of $\frac{dP}{dt}$ with respect to $P$ , which will give us $\frac{d^2P}{dt^2}$ .
Calculate First Derivative: The first derivative of $(\frac{dP}{dt})$ with respect to $P$ is given by the derivative of the right-hand side of the equation with respect to $P$ . We apply the product rule and the chain rule to find this derivative: $\newline$ $(\frac{d^2P}{dt^2}) = \frac{d}{dP} \left[\frac{2881}{7178}P\left(1 - \frac{P}{536}\right)\right]$ $\newline$ Let's denote $\frac{2881}{7178}$ as a constant $k$ for simplicity: $\newline$ $k = \frac{2881}{7178}$ $\newline$ Now, we differentiate: $\newline$ $(\frac{d^2P}{dt^2}) = k * \frac{d}{dP} \left[P - \frac{P^2}{536}\right]$ $\newline$ $(\frac{d^2P}{dt^2}) = k * \left(1 - \frac{2P}{536}\right)$
Set Second Derivative to Zero: To find the inflection point, we set the second derivative equal to zero and solve for $P$ : $0 = k \times \left(1 - \frac{2P}{536}\right)$ Since $k$ is a positive constant, we can divide both sides by $k$ without changing the inequality: $0 = 1 - \frac{2P}{536}$ Now, we solve for $P$ : $\frac{2P}{536} = 1$ $2P = 536$ $P = \frac{536}{2}$ $P = 268$
Solve for Inflection Point: We have found that the second derivative changes sign at $P = 268$ . This is the value of $P$ at which the graph of $P(t)$ has an inflection point.

More problems from Find derivatives using logarithmic differentiation

Question

\newline

\sqrt{\frac{9}{25}}

\newline

Posted 3 months ago

Question

\newline

1,000

\text{ milligrams}

\_\_\_\_

\text{ grams}

Posted 3 months ago

Question

3

-gallon bottle of bleach costs

\$11.52

. What is the price per quart?

\newline

Posted 3 months ago

Question

Maureen can't wait to make chocolate chip zucchini bread with zucchini from her garden. Her recipe calls for

8

ounces of chocolate chips per loaf. If she has enough zucchini to make

4

loaves of zucchini bread, how many pounds of chocolate chips does she need?

\newline

Hint: There are

16

1

\newline

Write your answer as a whole number, decimal, or simplified fraction. Do not round.

\newline

Posted 3 months ago

Question

A whale is swimming due north at a speed of

30

miles per hour. Just

5

miles away, a whale-watching tour boat is traveling south, directly toward the whale, at a speed of

46

miles per hour. How long will it be before they meet? If necessary, round your answer to the nearest minute.

\_\_\_\_

\_\_\_\_

Posted 3 months ago

Question

\newline

500

=

Posted 4 months ago

Question

\newline

2,000

=

Posted 4 months ago

Question

\newline

750

=

Posted 4 months ago

Question

\newline

1,500

=

Posted 4 months ago

Question

\newline

1,500

=

Posted 4 months ago