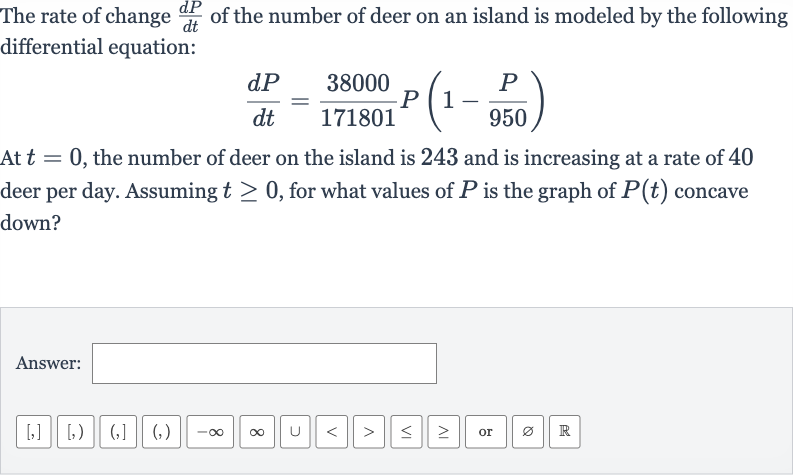
The rate of change (dP)/(dt) of the number of fox at a national park is modeled by the following differential equation: (dP)/(dt)=(3277)/(16290)P(1-(P)/( 904)) At t=0, the number of fox at the national park is 180 and is increasing at a rate of 29 fox per day. Find lim_(t rarr oo)P^(')(t). Answer:

Question

The rate of change  (dP)/(dt) of the number of fox at a national park is modeled by the following differential equation:  (dP)/(dt)=(3277)/(16290)P(1-(P)/( 904)) At  t=0, the number of fox at the national park is 180 and is increasing at a rate of 29 fox per day. Find  lim_(t rarr oo)P^(')(t). Answer:

Bytelearn · Accepted Answer

Identify Equation and Equilibrium: Identify the differential equation and the equilibrium point. The given differential equation is (dP)/(dt) = (3277)/(16290)P(1 - (P)/(904)). This is a logistic growth model where the growth rate of the population of foxes is proportional to both the current population P and the difference between the current population and the carrying capacity, which in this case is 904.Determine Equilibrium Points: Determine the equilibrium points. The equilibrium points occur when the growth rate (dP)/(dt) is zero. Setting the right-hand side of the differential equation to zero, we get (3277)/(16290)P(1 - (P)/(904)) = 0. This gives us two equilibrium points: P = 0 and P = 904.Analyze Stability: Analyze the stability of the equilibrium points. For logistic equations, the lower equilibrium point (P = 0) is usually unstable, and the upper equilibrium point (P = 904) is stable. This means that if the population starts above zero, it will tend to move towards the carrying capacity over time.Calculate Limit: Calculate the limit of P'(t) as t approaches infinity. Since the population is increasing and the carrying capacity is 904, the population will approach this carrying capacity as t approaches infinity. Therefore, the rate of change of the population (dP)/(dt) will approach zero as the population approaches the carrying capacity. Thus, lim_(t rarr oo)P^(')(t) = 0.

Full solution

More problems from Write and solve direct variation equations

Related topics