Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

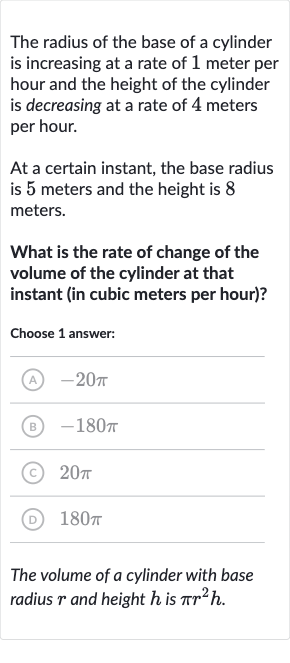
The radius of the base of a cylinder is increasing at a rate of 1 meter per hour and the height of the cylinder is decreasing at a rate of 4 meters per hour. At a certain instant, the base radius is 5 meters and the height is 8 meters. What is the rate of change of the volume of the cylinder at that instant (in cubic meters per hour)? Choose 1 answer: (A) -20 pi (B) -180 pi (C) 20 pi (D) 180 pi The volume of a cylinder with base radius r and height h is pir^(2)h.

The radius of the base of a cylinder is increasing at a rate of 11 meter per hour and the height of the cylinder is decreasing at a rate of 44 meters per hour.\newlineAt a certain instant, the base radius is 55 meters and the height is 88 meters.\newlineWhat is the rate of change of the volume of the cylinder at that instant (in cubic meters per hour)?\newlineChoose 11 answer:\newline(A) −20π -20 \pi \newline(B) −180π -180 \pi \newline(C) 20π 20 \pi \newline(D) 180π 180 \pi \newlineThe volume of a cylinder with base radius r r and height h h is πr2h \pi r^{2} h .

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 6right chevron icon
Area of quadrilaterals and triangles: word problemsright chevron icon

Full solution

Q. The radius of the base of a cylinder is increasing at a rate of 11 meter per hour and the height of the cylinder is decreasing at a rate of 44 meters per hour.\newlineAt a certain instant, the base radius is 55 meters and the height is 88 meters.\newlineWhat is the rate of change of the volume of the cylinder at that instant (in cubic meters per hour)?\newlineChoose 11 answer:\newline(A) −20π -20 \pi \newline(B) −180π -180 \pi \newline(C) 20π 20 \pi \newline(D) 180π 180 \pi \newlineThe volume of a cylinder with base radius r r and height h h is πr2h \pi r^{2} h .
  1. Volume Formula: The formula for the volume of a cylinder is V=πr2hV = \pi r^2 h. We need to find the rate of change of the volume, which is dVdt\frac{dV}{dt}.
  2. Chain Rule Application: To find dVdt\frac{dV}{dt}, we use the chain rule from calculus: dVdt=dVdr⋅drdt+dVdh⋅dhdt\frac{dV}{dt} = \frac{dV}{dr} \cdot \frac{dr}{dt} + \frac{dV}{dh} \cdot \frac{dh}{dt}.
  3. Calculate dV/drdV/dr: First, we find dV/drdV/dr which is the derivative of VV with respect to rr. dV/dr=2πrhdV/dr = 2\pi rh.
  4. Calculate dVdh\frac{dV}{dh}: Then we find dVdh\frac{dV}{dh} which is the derivative of VV with respect to hh. dVdh=πr2\frac{dV}{dh} = \pi r^2.
  5. Find drdt\frac{dr}{dt} and dhdt\frac{dh}{dt}: Now we plug in the values for drdt\frac{dr}{dt} and dhdt\frac{dh}{dt}. drdt\frac{dr}{dt} is 11 meter per hour and dhdt\frac{dh}{dt} is −4-4 meters per hour.
  6. Plug in Values: We also plug in the values for rr and hh at the instant we are considering. rr is 55 meters and hh is 88 meters.
  7. Calculate dVdt\frac{dV}{dt}: Now we calculate dVdt\frac{dV}{dt} using the values we have. dVdt=2π(5 meters)(8 meters)(1 meter/hour)+π(5 meters)2(−4 meters/hour)\frac{dV}{dt} = 2\pi(5 \text{ meters})(8 \text{ meters})(1 \text{ meter/hour}) + \pi(5 \text{ meters})^2(-4 \text{ meters/hour}).
  8. Simplify Expression: Simplify the expression. dVdt=80π\frac{dV}{dt} = 80\pi meters3^3/hour + (−100π)(-100\pi) meters3^3/hour.
  9. Combine Terms: Combine the terms to find the total rate of change of the volume. dVdt=80π−100π\frac{dV}{dt} = 80\pi - 100\pi meters3^3/hour.
  10. Final Result: Simplify the result. dVdt=−20π\frac{dV}{dt} = -20\pi meters3^3/hour.

More problems from Area of quadrilaterals and triangles: word problems

Question
The work done by stretching a certain spring increases by 0.13x 0.13 x joules per centimeter (where x x is the displacement, in centimeters, beyond the spring's natural length).\newlineHow much work (in Joules) must be done in order to stretch the spring from x=4 x=4 to x=10 x=10 ?\newlineChoose 11 answer:\newline(A) 55.4646\newline(B) 77.5454\newline(C) 10.92 \mathbf{1 0 . 9 2} \newline(D) 15.08 \mathbf{1 5 . 0 8}
Get tutor helpright-arrow

Posted 9 months ago

Question
Ahmed is modeling the area covered by a moss using the following equation:\newlineA=t2+5.8t+9.41 A=t^{2}+5.8 t+9.41 \newlinewhere A A is the area covered in square centimeters, negative values of t t represent a number of days before noon on July 11 , 20142014 , and positive values of t t represent a number of days after noon on July 11,20142014 . Which of the following equivalent expressions contains the number of days before noon on July 11,20142014 , as a constant or coefficient, when the moss started with its smallest area of 11 square centimeter?\newlineChoose 11 answer:\newline(A) (t−(−2.9))2+1 (t-(-2.9))^{2}+1 \newline(B) (t−(−1))2+3.8t+8.41 (t-(-1))^{2}+3.8 t+8.41 \newline(C) (t−(−3.9))(t−(−1.9))+2 (t-(-3.9))(t-(-1.9))+2 \newline(D) t(t−(−5.8))+9.41 t(t-(-5.8))+9.41
Get tutor helpright-arrow

Posted 9 months ago

Question
Solve.\newlineFind the exact volume and surface area of a sphere of radius 1212 inches.\newlineV=576π cu in.;V=576\pi\text{ cu in.}; SA=2304π sq in.SA=2304\pi\text{ sq in.}\newlineV=2304π cu in.;V=2304\pi\text{ cu in.}; SA=576π sq in.SA=576\pi\text{ sq in.}\newlineV=1728π cu inV=1728\pi\text{ cu in} ;SA=144π sq in.;SA=144\pi\text{ sq in.}\newlineV=6912π cuin.:V=6912\pi\text{ cuin.}:SA⋅=36π sq in.SA^{\cdot}=36\pi\text{ sq in.}\newline
Get tutor helpright-arrow

Posted 8 months ago

Question
What is the height of the tent?
Get tutor helpright-arrow

Posted 8 months ago

Question
The volume of a rectangular prism is 108 cm3 108 \mathrm{~cm}^{3} . Eric measures the sides to be 3.32 cm 3.32 \mathrm{~cm} by 4.04 cm 4.04 \mathrm{~cm} by 8.72 cm 8.72 \mathrm{~cm} . In calculating the volume, what is the relative error, to the nearest thousandth.\newlineAnswer:
Get tutor helpright-arrow

Posted 8 months ago

Question
In △UVW,w=8.9 \triangle \mathrm{UVW}, w=8.9 inches, v=9 v=9 inches and ∠V=50∘ \angle \mathrm{V}=50^{\circ} . Find all possible values of ∠W \angle \mathrm{W} , to the nearest 1010th of a degree.\newlineAnswer:
Get tutor helpright-arrow

Posted 8 months ago

Question
Circle O O shown below has a radius of 77 inches. To the nearest tenth of an inch, determine the length of the arc, x x , subtended by an angle of 11.44 radians.\newlineAnswer: □\square inches
Get tutor helpright-arrow

Posted 8 months ago

Question
Circle O O shown below has an arc of length 1919 inches subtended by an angle of 11 radians. Find the length of the radius, x x , to the nearest tenth of an inch.\newlineAnswer: □\square inches
Get tutor helpright-arrow

Posted 8 months ago

Question
The area of a rectangular goat pen is 54 square meters54 \, \text{square meters}. The perimeter is 30 meters30 \, \text{meters}. What are the dimensions of the pen?\newline____\_\_\_\_ meters by ____\_\_\_\_ meters
Get tutor helpright-arrow

Posted 8 months ago

Question
The perimeter of a square piece of tissue paper is 3636 centimeters. How long is each side of the tissue paper?\newline​_____ centimeters
Get tutor helpright-arrow

Posted 8 months ago

View all (25)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant