Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

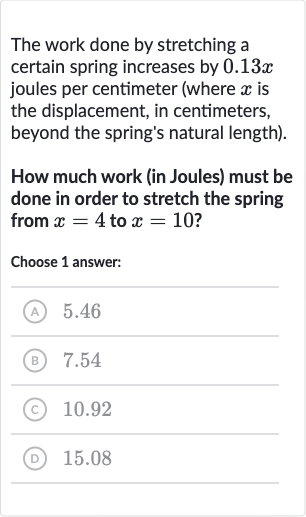
The work done by stretching a certain spring increases by
0.13 x joules per centimeter (where
x is the displacement, in centimeters, beyond the spring's natural length).
How much work (in Joules) must be done in order to stretch the spring from
x=4 to
x=10 ?
Choose 1 answer:
(A) 5.46
(B) 7.54
(C)
10.92
(D)
15.08

The work done by stretching a certain spring increases by $0.13 x$ joules per centimeter (where $x$ is the displacement, in centimeters, beyond the spring's natural length). $\newline$ How much work (in Joules) must be done in order to stretch the spring from $x=4$ to $x=10$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $5$ . $46$ $\newline$ (B) $7$ . $54$ $\newline$ (C) $\mathbf{1 0 . 9 2}$ $\newline$ (D) $\mathbf{1 5 . 0 8}$

View step-by-step help

View step-by-step help

Area of quadrilaterals and triangles: word problems

Full solution

Q. The work done by stretching a certain spring increases by

0.13 x

joules per centimeter (where

x

is the displacement, in centimeters, beyond the spring's natural length).

\newline

How much work (in Joules) must be done in order to stretch the spring from

x=4

to

x=10

?

\newline

Choose

1

answer:

\newline

(A)

5

.

46

\newline

(B)

7

.

54

\newline

(C)

\mathbf{1 0 . 9 2}

\newline

(D)

\mathbf{1 5 . 0 8}

Understand the problem: Understand the problem. $\newline$ We are given a spring where the work done to stretch it increases by $0.13$ times the displacement in joules per centimeter. We need to calculate the total work done when the spring is stretched from $4\,\text{cm}$ to $10\,\text{cm}$ .
Set up the integral: Set up the integral to calculate the work done. $\newline$ The work done on the spring from $x=4$ to $x=10$ can be calculated by integrating the work done per centimeter over the displacement. The integral will be from $4$ to $10$ of $0.13x \, dx$ .
Calculate the integral: Calculate the integral. $\newline$ The integral of $0.13x$ with respect to $x$ is $0.13 \times (x^2/2)$ . We need to evaluate this from $x=4$ to $x=10$ .
Evaluate the integral: Evaluate the integral from $x=4$ to $x=10$ . Plugging in the values we get: $0.13 \times (10^2/2) - 0.13 \times (4^2/2)$ = $0.13 \times (100/2) - 0.13 \times (16/2)$ = $0.13 \times 50 - 0.13 \times 8$ = $6.5 - 1.04$ = $5.46$ joules

More problems from Area of quadrilaterals and triangles: word problems

Question

Ahmed is modeling the area covered by a moss using the following equation:

\newline

A=t^{2}+5.8 t+9.41

\newline

A

is the area covered in square centimeters, negative values of

t

represent a number of days before noon on July

1

2014

, and positive values of

t

represent a number of days after noon on July

1

2014

. Which of the following equivalent expressions contains the number of days before noon on July

1

2014

, as a constant or coefficient, when the moss started with its smallest area of

1

square centimeter?

\newline

1

\newline

(t-(-2.9))^{2}+1

\newline

(t-(-1))^{2}+3.8 t+8.41

\newline

(t-(-3.9))(t-(-1.9))+2

\newline

t(t-(-5.8))+9.41

Posted 9 months ago

Question

\newline

Find the exact volume and surface area of a sphere of radius

12

\newline

V=576\pi\text{ cu in.};

SA=2304\pi\text{ sq in.}

\newline

V=2304\pi\text{ cu in.};

SA=576\pi\text{ sq in.}

\newline

V=1728\pi\text{ cu in}

;SA=144\pi\text{ sq in.}

\newline

V=6912\pi\text{ cuin.}:

SA^{\cdot}=36\pi\text{ sq in.}

\newline

Posted 8 months ago

Question

What is the height of the tent?

Posted 8 months ago

Question

The volume of a rectangular prism is

108 \mathrm{~cm}^{3}

. Eric measures the sides to be

3.32 \mathrm{~cm}

4.04 \mathrm{~cm}

8.72 \mathrm{~cm}

. In calculating the volume, what is the relative error, to the nearest thousandth.

\newline

Posted 8 months ago

Question

\triangle \mathrm{UVW}, w=8.9

v=9

\angle \mathrm{V}=50^{\circ}

. Find all possible values of

\angle \mathrm{W}

, to the nearest

10

th of a degree.

\newline

Posted 8 months ago

Question

O

shown below has a radius of

7

inches. To the nearest tenth of an inch, determine the length of the arc,

x

, subtended by an angle of

1

4

\newline

\square

Posted 8 months ago

Question

O

shown below has an arc of length

19

inches subtended by an angle of

1

radians. Find the length of the radius,

x

, to the nearest tenth of an inch.

\newline

\square

Posted 8 months ago

Question

The area of a rectangular goat pen is

54 \, \text{square meters}

. The perimeter is

30 \, \text{meters}

. What are the dimensions of the pen?

\newline

\_\_\_\_

\_\_\_\_

Posted 8 months ago

Question

The perimeter of a square piece of tissue paper is

36

centimeters. How long is each side of the tissue paper?

\newline

_____ centimeters

Posted 8 months ago

Question

You pick a card at random, put it back, and then pick another card at random.

\newline

4

\newline

5

\newline

6

\newline

7

\newline

What is the probability of picking a number greater than

5

and then picking a

4

\newline

Write your answer as a percentage.

Posted 1 month ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant