AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
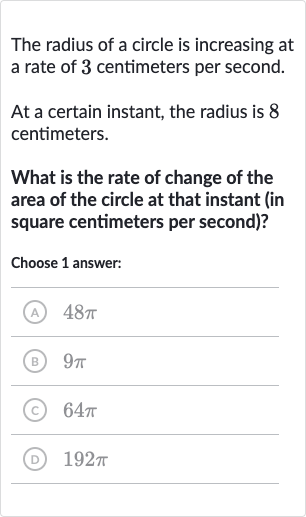
The radius of a circle is increasing at a rate of centimeters per second.At a certain instant, the radius is centimeters.What is the rate of change of the area of the circle at that instant (in square centimeters per second)?Choose answer:(A) (B) (C) (D)
Full solution
Q. The radius of a circle is increasing at a rate of centimeters per second.At a certain instant, the radius is centimeters.What is the rate of change of the area of the circle at that instant (in square centimeters per second)?Choose answer:(A) (B) (C) (D)
- Circle Area Formula: The formula for the area of a circle is , where is the area and is the radius.
- Differentiate Area with Respect to Time: To find the rate of change of the area, we need to differentiate the area with respect to time . So we get .
- Chain Rule Application: Using the chain rule, , where is the rate of change of the radius.
- Rate of Radius Change: We know the radius is increasing at a rate of centimeters per second, so .
- Plug in Values: Now we plug in the values:
- Simplify Calculation: Simplify the calculation: .
- Final Result: Finally, we get .
More problems from Area of quadrilaterals and triangles: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
