Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

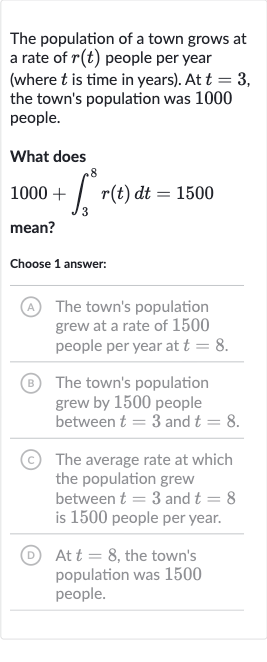
The population of a town grows at a rate of r(t) people per year (where t is time in years). At t=3, the town's population was 1000 people. What does 1000+int_(3)^(8)r(t)dt=1500 mean? Choose 1 answer: (A) The town's population grew at a rate of 1500 people per year at t=8. (B) The town's population grew by 1500 people between t=3 and t=8. (C) The average rate at which the population grew between t=3 and t=8 is 1500 people per year. (D) At t=8, the town's population was 1500 people.

The population of a town grows at a rate of r(t) r(t) people per year (where t t is time in years). At t=3 t=3 , the town's population was 10001000 people.\newlineWhat does 1000+∫38r(t)dt=1500 1000+\int_{3}^{8} r(t) d t=1500 mean?\newlineChoose 11 answer:\newline(A) The town's population grew at a rate of 15001500 people per year at t=8 t=8 .\newline(B) The town's population grew by 15001500 people between t=3 t=3 and t=8 t=8 .\newline(C) The average rate at which the population grew between t=3 t=3 and t=8 t=8 is 15001500 people per year.\newline(D) At t=8 t=8 , the town's population was 15001500 people.

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find derivatives of using multiple formulaeright chevron icon

Full solution

Q. The population of a town grows at a rate of r(t) r(t) people per year (where t t is time in years). At t=3 t=3 , the town's population was 10001000 people.\newlineWhat does 1000+∫38r(t)dt=1500 1000+\int_{3}^{8} r(t) d t=1500 mean?\newlineChoose 11 answer:\newline(A) The town's population grew at a rate of 15001500 people per year at t=8 t=8 .\newline(B) The town's population grew by 15001500 people between t=3 t=3 and t=8 t=8 .\newline(C) The average rate at which the population grew between t=3 t=3 and t=8 t=8 is 15001500 people per year.\newline(D) At t=8 t=8 , the town's population was 15001500 people.
  1. Evaluate Integral Meaning: Evaluate the meaning of the integral in the context of population growth. The integral ∫38r(t)dt\int_{3}^{8}r(t)dt represents the total change in population from time t=3t=3 to t=8t=8.
  2. Interpret Equation: Interpret the equation 1000+∫38r(t)dt=15001000 + \int_{3}^{8}r(t)dt = 1500. The initial population at t=3t=3 is 10001000 people. The integral adds the total population change from t=3t=3 to t=8t=8 to this initial population. The result, 15001500, is the population at t=8t=8.
  3. Determine Correct Answer Choice: Determine which answer choice correctly describes the equation.\newline(A) Incorrect - The equation does not describe the rate of population growth at t=8t=8.\newline(B) Correct - The equation indicates that the population grew by 500500 people (1500−10001500 - 1000) between t=3t=3 and t=8t=8.\newline(C) Incorrect - The equation does not provide information about the average rate of growth.\newline(D) Incorrect - The equation states that the population is 15001500 at t=8t=8, not that it grew by 15001500 people.

More problems from Find derivatives of using multiple formulae

Question
Find lim⁡θ→π2tan⁡2(θ)[1−sin⁡(θ)] \lim_{\theta \rightarrow \frac{\pi}{2}} \tan ^{2}(\theta)[1-\sin (\theta)] .\newlineChoose 11 answer:\newline(A) 00\newline(B) 12 \frac{1}{2} \newline(C) −2-2\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 9 months ago

Question
Find lim⁡θ→π2sin⁡2(2θ)1−sin⁡2(θ) \lim _{\theta \rightarrow \frac{\pi}{2}} \frac{\sin ^{2}(2 \theta)}{1-\sin ^{2}(\theta)} \newlineChoose 11 answer:\newline(A) 11\newline(B) 22\newline(C) 44\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 9 months ago

Question
Find lim⁡x→3x−34x+4−4 \lim _{x \rightarrow 3} \frac{x-3}{\sqrt{4 x+4}-4} .\newlineChoose 11 answer:\newline(A) −4-4\newline(B) 11\newline(C) 22\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 9 months ago

Question
Find lim⁡x→−47x+28x2+x−12 \lim _{x \rightarrow-4} \frac{7 x+28}{x^{2}+x-12} .\newlineChoose 11 answer:\newline(A) 11\newline(B) 77\newline(C) −1-1\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 9 months ago

Question
Find lim⁡x→−3x+34−2x+22 \lim _{x \rightarrow-3} \frac{x+3}{4-\sqrt{2 x+22}} .\newlineChoose 11 answer:\newline(A) −3-3\newline(B) −4-4\newline(C) −34 -\frac{3}{4} \newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 9 months ago

Question
Find lim⁡x→15x+4−3x−1 \lim _{x \rightarrow 1} \frac{\sqrt{5 x+4}-3}{x-1} .\newlineChoose 11 answer:\newline(A) 35 \frac{3}{5} \newline(B) 56 \frac{5}{6} \newline(C) 11\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 9 months ago

Question
Find lim⁡x→−2x3+3x2+2xx+2 \lim _{x \rightarrow-2} \frac{x^{3}+3 x^{2}+2 x}{x+2} .\newlineChoose 11 answer:\newline(A) 66\newline(B) 00\newline(C) 22\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 9 months ago

Question
Find lim⁡x→π2cot⁡2(x)1−sin⁡(x) \lim _{x \rightarrow \frac{\pi}{2}} \frac{\cot ^{2}(x)}{1-\sin (x)} \newlineChoose 11 answer:\newline(A) −1-1\newline(B) −π2 -\frac{\pi}{2} \newline(C) 22\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 9 months ago

Question
Find lim⁡x→π2sin⁡(2x)cos⁡(x) \lim _{x \rightarrow \frac{\pi}{2}} \frac{\sin (2 x)}{\cos (x)} .\newlineChoose 11 answer:\newline(A) 12 \frac{1}{2} \newline(B) 11\newline(C) 22\newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 9 months ago

Question
Find lim⁡θ→π4cos⁡(2θ)2cos⁡(θ)−1 \lim _{\theta \rightarrow \frac{\pi}{4}} \frac{\cos (2 \theta)}{\sqrt{2} \cos (\theta)-1} .\newlineChoose 11 answer:\newline(A) 22\newline(B) 12 \frac{1}{2} \newline(C) 2 \sqrt{2} \newline(D) The limit doesn't exist
Get tutor helpright-arrow

Posted 9 months ago

View all (82)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant