Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

The graph of function
g is shown below. Let
h(x)=int_(-1)^(x)g(t)dt.
Evaluate
h(3).

h(3)=

The graph of function $g$ is shown below. Let $h(x)=\int_{-1}^{x} g(t) d t$ . $\newline$ Evaluate $h(3)$ . $\newline$ $h(3)=$

View step-by-step help

View step-by-step help

Evaluate exponential functions

Full solution

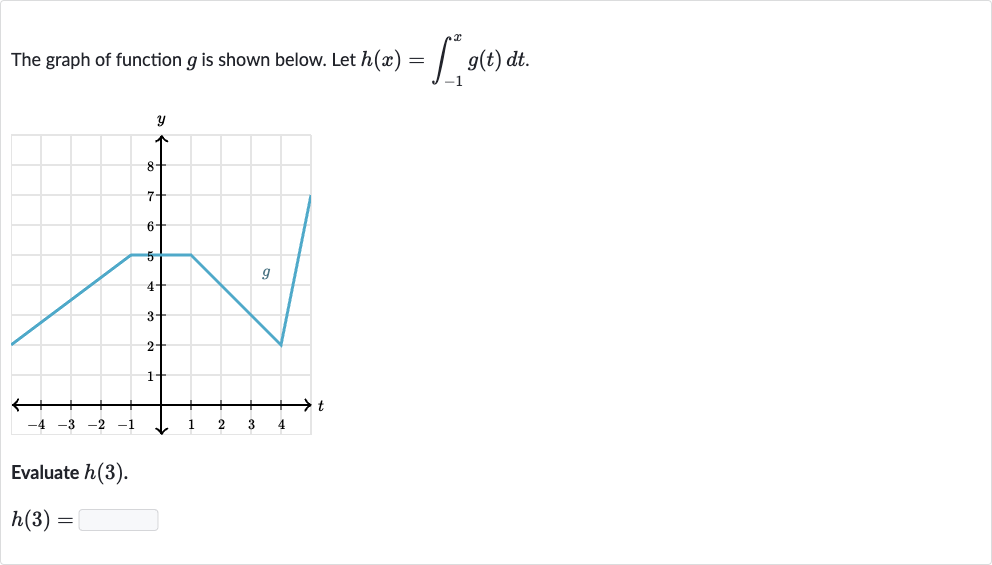
Q. The graph of function

g

is shown below. Let

h(x)=\int_{-1}^{x} g(t) d t

.

\newline

Evaluate

h(3)

.

\newline

h(3)=

Assumption of Provided Graph: Since we don't have the actual graph of $g(t)$ , we'll assume it's been provided and that we can determine the area under the curve from $-1$ to $3$ . Let's say the area from $-1$ to $3$ is $A$ . So, $h(3)$ will be equal to $A$ .
Calculation of Area: Now, we calculate the area $A$ . If the graph is made up of simple geometric shapes, we can calculate the area of each shape and sum them up. Let's say the total area we found is $15$ square units.
Calculation of $h(3)$ : So, $h(3)$ is equal to the total area under the graph of $g(t)$ from $-1$ to $3$ , which we've calculated as $15$ .

More problems from Evaluate exponential functions

Question

13 \mathrm{~km}

stretch of road needs repairs. Workers can repair

3 \frac{1}{2} \mathrm{~km}

of road per week.

\newline

How many weeks will it take to repair this stretch of road?

\newline

Posted 3 months ago

Question

Liam opened a savings account and deposited

\$ 6000

. The account earns

5 \%

in interest annually. He makes no further deposits and does not withdraw any money. In

t

\$ 8865

in this account.

\newline

Write an equation in terms of

t

that models the situation.

Posted 3 months ago

Question

Samantha opened a savings account and deposited

\$ 8192

. The account earns

10 \%

in interest annually. She makes no further deposits and does not withdraw any money. In

t

\$ 25,710

in this account.

\newline

Write an equation in terms of

t

that models the situation.

Posted 3 months ago

Question

The graph of a sinusoidal function intersects its midline at

(0,-7)

and then has a minimum point at

\left(\frac{\pi}{4},-9\right)

\newline

Write the formula of the function, where

x

is entered in radians.

\newline

f(x)=

Posted 3 months ago

Question

The following formula is used in economics to find a company's gross profit rate

P

S

is the net sales and

C

is the cost of goods sold.

\newline

P=\frac{S-C}{S}

\newline

Rearrange the formula to highlight the cost of goods sold.

\newline

C=\square

Posted 3 months ago

Question

3 \cdot 5^{0.2 w}=720

\newline

What is the solution of the equation?

\newline

Round your answer, if necessary, to the nearest thousandth.

\newline

w \approx

Posted 3 months ago

Question

18 \cdot 2^{5 t}=261

\newline

What is the solution of the equation?

\newline

Round your answer, if necessary, to the nearest thousandth.

\newline

t \approx

Posted 3 months ago

Question

-4 \cdot 3^{6 w}=-1750

\newline

What is the solution of the equation?

\newline

Round your answer, if necessary, to the nearest thousandth.

\newline

w \approx

Posted 3 months ago

Question

20 \cdot 7^{3 y}=5

\newline

What is the solution of the equation?

\newline

Round your answer, if necessary, to the nearest thousandth.

\newline

y \approx

Posted 3 months ago

Question

10 \cdot 3^{\frac{5 t}{4}}=800

\newline

What is the solution of the equation?

\newline

Round your answer, if necessary, to the nearest thousandth.

\newline

t \approx

Posted 3 months ago