Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

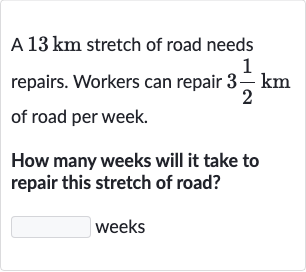
A 13km stretch of road needs repairs. Workers can repair 3(1)/(2)km of road per week. How many weeks will it take to repair this stretch of road? weeks

A 13 km 13 \mathrm{~km} stretch of road needs repairs. Workers can repair 312 km 3 \frac{1}{2} \mathrm{~km} of road per week.\newlineHow many weeks will it take to repair this stretch of road?\newlineweeks

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 2right chevron icon
Exponential growth and decay: word problemsright chevron icon

Full solution

Q. A 13 km 13 \mathrm{~km} stretch of road needs repairs. Workers can repair 312 km 3 \frac{1}{2} \mathrm{~km} of road per week.\newlineHow many weeks will it take to repair this stretch of road?\newlineweeks
  1. Given Data: We have:\newlineTotal length of road to repair: 13 km13\,\text{km}\newlineRepair rate per week: 312 km3\frac{1}{2}\,\text{km} or 3.5 km3.5\,\text{km}\newlineIdentify the values of total length and repair rate per week.\newlineTotal length (L)=13 km(L) = 13\,\text{km}\newlineRepair rate per week (R)=3.5 km(R) = 3.5\,\text{km}
  2. Find Weeks: We need to find:\newlineTotal number of weeks WW required to repair the 1313km stretch of road.\newlineIdentify the formula to calculate the total number of weeks.\newlineThe formula is W=LRW = \frac{L}{R}.\newlineSubstitute L=13L = 13km and R=3.5R = 3.5km in W=LRW = \frac{L}{R}.\newlineW=133.5W = \frac{13}{3.5}
  3. Calculate Weeks: Let's simplify the division to find the number of weeks.\newlineCalculate 13/3.513 / 3.5.\newline13/3.5=3.71428571…13 / 3.5 = 3.71428571\dots\newlineSince the number of weeks must be a whole number, we round up because workers cannot repair a fraction of a week.\newlineW=4W = 4
  4. Final Result: The total number of weeks required to repair the 1313km stretch of road is 44 weeks.

More problems from Exponential growth and decay: word problems

Question
Liam opened a savings account and deposited $6000 \$ 6000 . The account earns 5% 5 \% in interest annually. He makes no further deposits and does not withdraw any money. In t t years, he has $8865 \$ 8865 in this account.\newlineWrite an equation in terms of t t that models the situation.
Get tutor helpright-arrow

Posted 3 months ago

Question
Samantha opened a savings account and deposited $8192 \$ 8192 . The account earns 10% 10 \% in interest annually. She makes no further deposits and does not withdraw any money. In t t years, she has $25,710 \$ 25,710 in this account.\newlineWrite an equation in terms of t t that models the situation.
Get tutor helpright-arrow

Posted 3 months ago

Question
The graph of a sinusoidal function intersects its midline at (0,−7) (0,-7) and then has a minimum point at (π4,−9) \left(\frac{\pi}{4},-9\right) .\newlineWrite the formula of the function, where x x is entered in radians.\newlinef(x)= f(x)=
Get tutor helpright-arrow

Posted 3 months ago

Question
The following formula is used in economics to find a company's gross profit rate P P , where S S is the net sales and C C is the cost of goods sold.\newlineP=S−CS P=\frac{S-C}{S} \newlineRearrange the formula to highlight the cost of goods sold.\newlineC=□ C=\square
Get tutor helpright-arrow

Posted 3 months ago

Question
3⋅50.2w=720 3 \cdot 5^{0.2 w}=720 \newlineWhat is the solution of the equation?\newlineRound your answer, if necessary, to the nearest thousandth.\newlinew≈ w \approx
Get tutor helpright-arrow

Posted 3 months ago

Question
18⋅25t=261 18 \cdot 2^{5 t}=261 \newlineWhat is the solution of the equation?\newlineRound your answer, if necessary, to the nearest thousandth.\newlinet≈ t \approx
Get tutor helpright-arrow

Posted 3 months ago

Question
−4⋅36w=−1750 -4 \cdot 3^{6 w}=-1750 \newlineWhat is the solution of the equation?\newlineRound your answer, if necessary, to the nearest thousandth.\newlinew≈ w \approx
Get tutor helpright-arrow

Posted 3 months ago

Question
20⋅73y=5 20 \cdot 7^{3 y}=5 \newlineWhat is the solution of the equation?\newlineRound your answer, if necessary, to the nearest thousandth.\newliney≈ y \approx
Get tutor helpright-arrow

Posted 3 months ago

Question
10⋅35t4=800 10 \cdot 3^{\frac{5 t}{4}}=800 \newlineWhat is the solution of the equation?\newlineRound your answer, if necessary, to the nearest thousandth.\newlinet≈ t \approx
Get tutor helpright-arrow

Posted 3 months ago

Question
56x856x8
Get tutor helpright-arrow

Posted 8 hours ago

View all (3)