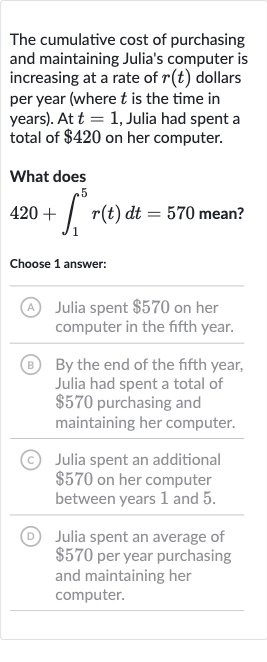
The cumulative cost of purchasing and maintaining Julia's computer is increasing at a rate of r(t) dollars per year (where t is the time in years). At t=1, Julia had spent a total of $420 on her computer. What does 420+int_(1)^(5)r(t)dt=570 mean? Choose 1 answer: (A) Julia spent $570 on her computer in the fifth year. (B) By the end of the fifth year, Julia had spent a total of $570 purchasing and maintaining her computer. (C) Julia spent an additional $570 on her computer between years 1 and 5 . (D) Julia spent an average of $570 per year purchasing and maintaining her computer.

Question

The cumulative cost of purchasing and maintaining Julia's computer is increasing at a rate of  r(t) dollars per year (where  t is the time in years). At  t=1, Julia had spent a total of  $420 on her computer. What does  420+int_(1)^(5)r(t)dt=570 mean? Choose 1 answer: (A) Julia spent  $570 on her computer in the fifth year. (B) By the end of the fifth year, Julia had spent a total of  $570 purchasing and maintaining her computer. (C) Julia spent an additional  $570 on her computer between years 1 and 5 . (D) Julia spent an average of  $570 per year purchasing and maintaining her computer.

Bytelearn · Accepted Answer

Given Equation Interpretation: We are given the equation 420 + ∫_(1)^(5)r(t)dt = 570. This equation includes an integral, which represents the total additional cost from time t=1 to t=5. The initial value 420 represents the total cost at t=1. The equation is setting the sum of the initial cost and the additional cost over the next four years equal to 570.Integral Meaning: To understand what the equation means, we need to interpret the integral. The integral ∫_(1)^(5)r(t)dt represents the total additional cost of purchasing and maintaining the computer from year 1 to year 5. It does not represent the cost in any single year, but the cumulative additional cost over those years.Total Cost Calculation: Adding the initial cost of $420 to the integral gives us the total cost by the end of year 5. Therefore, the equation 420 + ∫_(1)^(5)r(t)dt = 570 means that by the end of the fifth year, Julia had spent a total of $570 on her computer.Answer Choice Evaluation A: Now we can evaluate the answer choices given: (A) This choice suggests that Julia spent $570 in the fifth year alone, which is incorrect because the integral represents the cumulative additional cost from years 1 to 5, not the cost in the fifth year only.Answer Choice Evaluation B: (B) This choice is correct because it states that by the end of the fifth year, Julia had spent a total of $570 on her computer, which is exactly what the equation represents.Answer Choice Evaluation C: (C) This choice is incorrect because it suggests that Julia spent an additional $570 between years 1 and 5, but the total amount spent by the end of year 5 is $570, not the additional amount spent.Answer Choice Evaluation D: (D) This choice is incorrect because it suggests an average yearly cost, which cannot be determined from the given equation without additional information about the function r(t).

Full solution

More problems from Solve radical equations

Related topics