AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
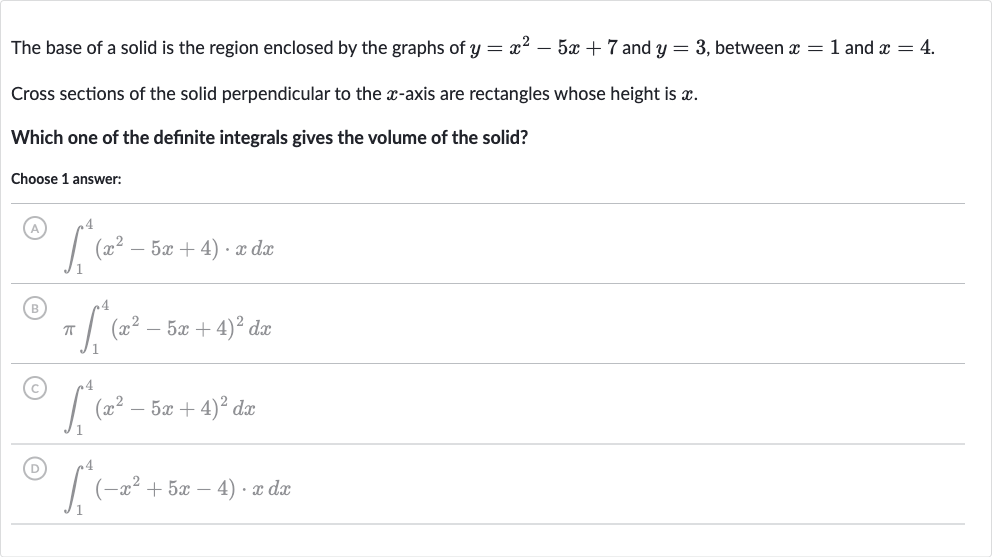
The base of a solid is the region enclosed by the graphs of and , between and .Cross sections of the solid perpendicular to the -axis are rectangles whose height is .Which one of the definite integrals gives the volume of the solid?Choose answer:(A) (B) (C) (D)
Full solution
Q. The base of a solid is the region enclosed by the graphs of and , between and .Cross sections of the solid perpendicular to the -axis are rectangles whose height is .Which one of the definite integrals gives the volume of the solid?Choose answer:(A) (B) (C) (D)
- Define Volume Integral: To find the volume of the solid, we need to integrate the area of the cross-sections along the -axis from to . The area of each rectangular cross-section is given by the difference in the -values of the two functions ( and ) times the height of the rectangle, which is . So, the area of a cross-section at a point is .
- Simplify Area Expression: First, simplify the expression for by distributing and combining like terms:
- Integrate to Find Volume: Now, we need to integrate from to to find the volume of the solid:This corresponds to one of the answer choices.
- Match with Answer Choices: Comparing the integral we found with the answer choices, we see that it matches with choice :
