AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
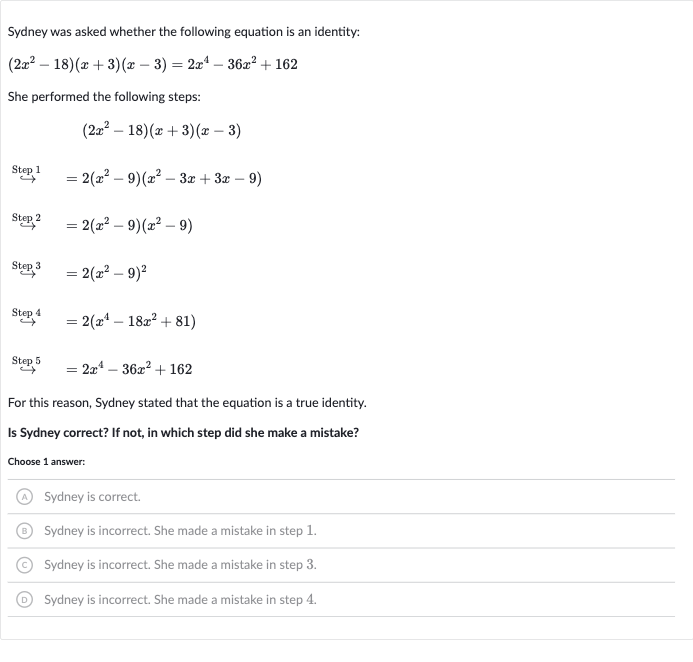
Sydney was asked whether the following equation is an identity:She performed the following steps:For this reason, Sydney stated that the equation is a true identity.Is Sydney correct? If not, in which step did she make a mistake?Choose answer:(A) Sydney is correct.(B) Sydney is incorrect. She made a mistake in step .(C) Sydney is incorrect. She made a mistake in step .(D) Sydney is incorrect. She made a mistake in step .
Full solution
Q. Sydney was asked whether the following equation is an identity:She performed the following steps:For this reason, Sydney stated that the equation is a true identity.Is Sydney correct? If not, in which step did she make a mistake?Choose answer:(A) Sydney is correct.(B) Sydney is incorrect. She made a mistake in step .(C) Sydney is incorrect. She made a mistake in step .(D) Sydney is incorrect. She made a mistake in step .
- Expand terms: Expand the first two terms and .
More problems from One-step inequalities: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
