Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

-11 x >= -33
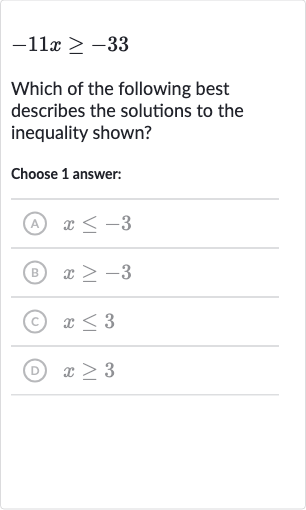
Which of the following best describes the solutions to the inequality shown?
Choose 1 answer:
(A)
x <= -3
(B)
x >= -3
(c)
x <= 3
(D)
x >= 3

$-11 x \geq-33$ $\newline$ Which of the following best describes the solutions to the inequality shown? $\newline$ Choose $1$ answer: $\newline$ (A) $x \leq-3$ $\newline$ (B) $x \geq-3$ $\newline$ (C) $x \leq 3$ $\newline$ (D) $x \geq 3$

View step-by-step help

View step-by-step help

Solutions to inequalities

Full solution

Q.

-11 x \geq-33

\newline

Which of the following best describes the solutions to the inequality shown?

\newline

Choose

1

answer:

\newline

(A)

x \leq-3

\newline

(B)

x \geq-3

\newline

(C)

x \leq 3

\newline

(D)

x \geq 3

Analyze the inequality: Analyze the inequality $-11x \geq -33$ . $\newline$ To find the solutions to the inequality, we need to isolate $x$ . We do this by dividing both sides of the inequality by $-11$ . Remember that when you divide or multiply both sides of an inequality by a negative number, you must reverse the direction of the inequality sign. $\newline$ $\frac{-11x}{-11} \leq \frac{-33}{-11}$
Divide both sides by ext{-} $11$ : Perform the division to solve for $x$ . $\newline$ $x \leq 3$
Perform the division to solve for $x$ : Match the solution to the given choices. $\newline$ The solution we found is $x \leq 3$ , which matches choice (C).

More problems from Solutions to inequalities

Question

\frac{3}{2} q \leq \frac{9}{2} q-18

\newline

Which of the following best describes the solutions to the inequality shown?

\newline

1

\newline

q \leq 3

\newline

q \geq 3

\newline

q \leq 6

\newline

q \geq 6

Posted 7 months ago

Question

g(x)=5-e^{x}

\newline

Below is Sean's attempt to write a formal justification for the fact that the equation

g(x)=0

has a solution where

1 \leq x \leq 4

\newline

Is Sean's justification complete? If not, why?

\newline

Sean's justification:

\newline

g

is defined for all real numbers, and exponential functions are continuous at all points in their domains.

\newline

So, according to the intermediate value theorem,

g(x)=0

must have a solution somewhere between

x=1

x=4

\newline

1

\newline

(A) Yes, Sean's justification is complete.

\newline

(B) No, Sean didn't establish that

0

g(1)

g(4)

\newline

(C) No, Sean didn't establish that

g

Posted 7 months ago

Question

f(x)=\sqrt[3]{\cos (\pi \cdot x)}

\newline

Below is Issac's attempt to write a formal justification for the fact that the equation

f(x)=0.1

has a solution where

1.5 \leq x \leq 2

\newline

Is Issac's justification complete? If not, why?

\newline

Issac's justification:

\newline

\begin{array}{l} f(1.5)=0 \text { and } \\ f(2)=1 \text {, so } \\ f(1.5)<0.1<f(2) . \end{array}

\newline

So, according to the intermediate value theorem,

f(x)=0.1

must have a solution when

x

x=1.5

x=2

\newline

1

\newline

(A) Yes, Issac's justification is complete.

\newline

(B) No, Issac didn't establish that

0

1

f(1.5)

f(2)

\newline

(C) No, Issac didn't establish that

f

Posted 7 months ago

Question

h(x)=5 \cdot \tan (x)

\newline

Below is Bridget's attempt to write a formal justification for the fact that the equation

h(x)=2

has a solution where

0 \leq x \leq \frac{\pi}{4}

\newline

Is Bridget's justification complete? If not, why?

\newline

Bridget's justification:

\newline

h

is defined over the entire interval

\left[0, \frac{\pi}{4}\right]

, and trigonometric functions are continuous at all points in their domains.

\newline

So, according to the intermediate value theorem,

h(x)=2

must have a solution at some point in that interval.

\newline

1

\newline

(A) Yes, Bridget's justification is complete.

\newline

(B) No, Bridget didn't establish that

2

h(0)

h\left(\frac{\pi}{4}\right)

\newline

(C) No, Bridget didn't establish that

h

Posted 7 months ago

Question

f(x)=2^{5-2 x}

\newline

Below is Ibrahim's attempt to write a formal justification for the fact that the equation

f(x)=10

has a solution where

-1 \leq x \leq 4

\newline

Is Ibrahim's justification complete? If not, why?

\newline

Ibrahim's justification:

\newline

f

is defined for all real numbers, and exponential functions are continuous at all points in their domains. Also,

f(-1)=128

f(4)=\frac{1}{8}

10

f(-1)

f(4)

\newline

So, according to the intermediate value theorem,

f(x)=10

must have a solution at some point between

x=-1

x=4

\newline

1

\newline

(A) Yes, Ibrahim's justification is complete.

\newline

(B) No, Ibrahim didn't establish that

10

f(-1)

f(4)

\newline

(c) No, Ibrahim didn't establish that

f

Posted 7 months ago

Question

g(x)=\cos \left(\pi x^{2}\right)

\newline

Below is Amrita's attempt to write a formal justification for the fact that the equation

g^{\prime}(x)=0.4

has a solution where

-1<x<4

\newline

Is Amrita's justification complete?

\newline

\newline

Amrita's justification:

\newline

Polynomial and trigonometric functions are differentiable and continuous at all points in their domain, and

[-1,4]

g^{\prime}

s domain. Also,

\newline

\begin{array}{l} g(-1)=-1 \text { and } \\ g(4)=1 \text {, so } \\ \frac{g(4)-g(-1)}{4-(-1)}=0.4 . \end{array}

\newline

So, according to the mean value theorem,

g^{\prime}(x)=0.4

must have a solution somewhere between

x=-1

x=4

\newline

1

\newline

(A) Yes, Amrita's justification is complete.

\newline

(B) No, Amrita didn't establish that the average rate of change of

g

[-1,4]

0

4

\newline

(C) No, Amrita didn't establish that

g

is differentiable.

Posted 7 months ago

Question

\newline

h(x)=x^{5}-2 x^{4}+10 x^{2}-10 x \text {. }

\newline

Below is Omar's attempt to write a formal justification for the fact that there exists a value

c

\newline

-2<c<2 \text { such that } h^{\prime}(c)=6 \text {. }

\newline

Is Omar's justification complete? If not, why?

\newline

Omar's justification:

\newline

\begin{array}{l} h(-2)=-4 \text { and } \\ h(2)=20 \text {, so } \\ \frac{h(2)-h(-2)}{2-(-2)}=6 . \end{array}

\newline

So, according to the mean value theorem, there exists a value

c

somewhere in the interval

-2<c<2

h^{\prime}(c)=6

\newline

1

\newline

(A) Yes, Omar's justification is complete.

\newline

(B) No, Omar didn't establish that the average rate of change of

h

[-2,2]

6

\newline

(C) No, Omar didn't establish that

h

is differentiable.

Posted 7 months ago

Question

f(x)=\sqrt{x+\sqrt{x^{3}}}

\newline

Below is Lena's attempt to write a formal justification for the fact that the equation

f^{\prime}(x)=\frac{2}{3}

has a solution where

0<x<9

\newline

Is Lena's justification complete? If not, why?

\newline

Lena's justification:

\newline

f(0)=0

f(9)=6

, so the average rate of change of

f

over the interval

0 \leq x \leq 9

\frac{2}{3}

\newline

So, according to the mean value theorem,

f^{\prime}(x)=\frac{2}{3}

must have a solution somewhere in the interval

0<x<9

\newline

1

\newline

(A) Yes, Lena's justification is complete.

\newline

(B) No, Lena didn't establish that the average rate of change of

f

[0,9]

\frac{2}{3}

\newline

(C) No, Lena didn't establish that

f

is differentiable.

Posted 7 months ago

Question

h(x)=3^{x}-x^{2}

\newline

Below is Uriah's attempt to write a formal justification for the fact that the equation

h^{\prime}(x)=8

has a solution where

1<x<3

\newline

Is Uriah's justification complete? If not, why?

\newline

Uriah's justification:

\newline

Polynomial and exponential functions are differentiable and continuous at all points in their domain, and

[1,3]

h

's domain. Also,

h(1)=2

h(3)=18

\newline

\frac{h(3)-h(1)}{3-1}=8 \text {. }

\newline

So, according to the mean value theorem,

h^{\prime}(x)=8

must have a solution somewhere between

x=1

x=3

\newline

1

\newline

(A) Yes, Uriah's justification is complete.

\newline

(B) No, Uriah didn't establish that the average rate of change of

h

[1,3]

8

\newline

(C) No, Uriah didn't establish that

h

is differentiable.

Posted 7 months ago

Question

18

6^{3-3 k}=\frac{1}{216}

Posted 19 hours ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant