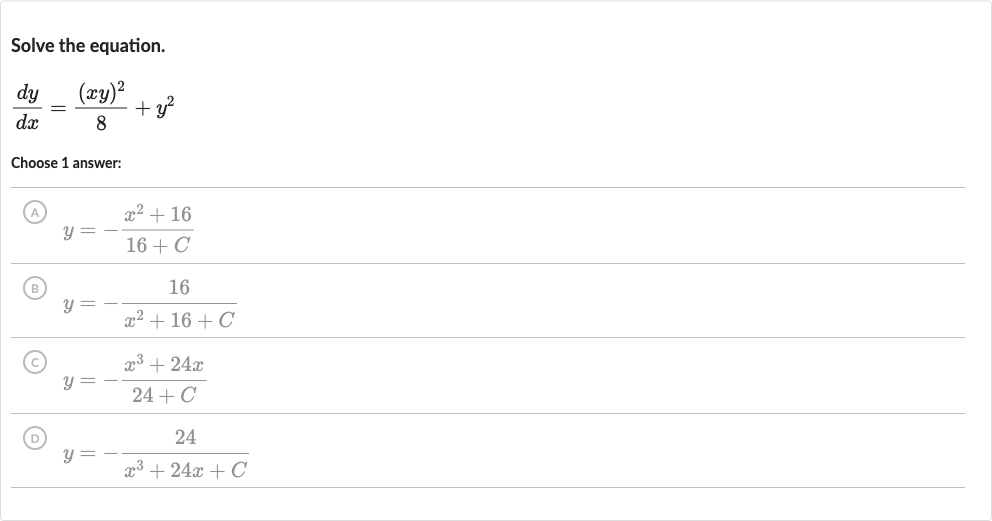
Solve the equation. (dy)/(dx)=((xy)^(2))/(8)+y^(2) Choose 1 answer: (A) y=-(x^(2)+16)/(16+C) (B) y=-(16)/(x^(2)+16+C) (C) y=-(x^(3)+24 x)/(24+C) (D) y=-(24)/(x^(3)+24 x+C)

Question

Solve the equation.  (dy)/(dx)=((xy)^(2))/(8)+y^(2) Choose 1 answer: (A)  y=-(x^(2)+16)/(16+C) (B)  y=-(16)/(x^(2)+16+C) (C)  y=-(x^(3)+24 x)/(24+C) (D)  y=-(24)/(x^(3)+24 x+C)

Bytelearn · Accepted Answer

Identify Equation Type: This is a first-order non-linear ordinary differential equation. To solve it, we will try to separate the variables x and y if possible.Rewrite Equation: First, let's rewrite the equation to make it clearer: (dy)/(dx) = (x^2 * y^2) / 8 + y^2Separate Variables: Now, we attempt to separate the variables by factoring out y^2 on the right side: (dy)/(dx) = y^2 * (x^2 / 8 + 1)Integrate Both Sides: Next, we divide both sides by y^2 and multiply by dx to get: (dy) / y^2 = (x^2 / 8 + 1) dxSolve for y: Now we integrate both sides of the equation. On the left side, we integrate with respect to y, and on the right side, we integrate with respect to x: ∫(1/y^2) dy = ∫(x^2 / 8 + 1) dxSimplify Expression: The integral of 1/y^2 with respect to y is -1/y. The integral of x^2/8 with respect to x is x^3/24, and the integral of 1 with respect to x is x. So we have: -1/y = x^3/24 + x + C, where C is the constant of integration.Replace Constant: We solve for y by taking the reciprocal of both sides and multiplying by -1: y = -1 / (x^3/24 + x + C)Final Solution: We can simplify the expression by multiplying the numerator and denominator by 24 to clear the fraction in the denominator: y = -24 / (x^3 + 24x + 24C)We can replace 24C with a new constant, let's call it C', since it is still an arbitrary constant: y = -24 / (x^3 + 24x + C')This matches answer choice (D), so the solution to the differential equation is: y = -24 / (x^3 + 24x + C')

Solve the equation. $\newline$ $\frac{d y}{d x}=\frac{(x y)^{2}}{8}+y^{2}$ $\newline$ Choose $1$ answer: $\newline$ (A) $y=-\frac{x^{2}+16}{16+C}$ $\newline$ (B) $y=-\frac{16}{x^{2}+16+C}$ $\newline$ (C) $y=-\frac{x^{3}+24 x}{24+C}$ $\newline$ (D) $y=-\frac{24}{x^{3}+24 x+C}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics