AI tutor
Full solution
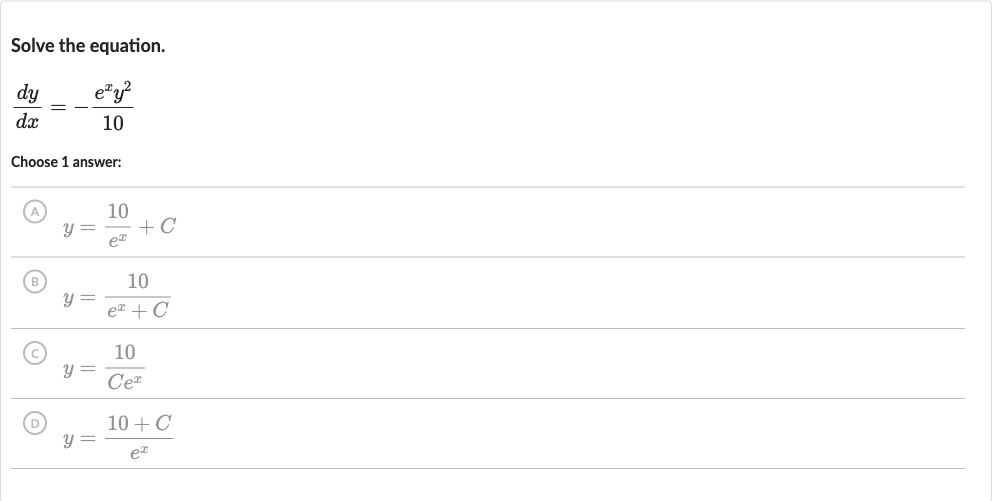
Q. Solve the equation.Choose answer:(A) (B) (C) (D)
- Separate variables: This is a first-order separable differential equation. To solve it, we need to separate the variables and on different sides of the equation.We can rewrite this as:
- Integrate both sides: Now we integrate both sides of the equation with respect to their variables.
- Apply constant of integration: The integral of with respect to is , and the integral of with respect to is ., where is the constant of integration.
- Take reciprocal: We multiply both sides by to get rid of the negative sign on the left side.
- Simplify expression: Now we take the reciprocal of both sides to solve for .
- Compare with options: To simplify the expression, we can multiply the numerator and denominator by .We can rename the constant to a new constant for simplicity.
- Compare with options: To simplify the expression, we can multiply the numerator and denominator by . We can rename the constant to a new constant for simplicity.We compare the final expression with the given options.The correct answer is (B) .