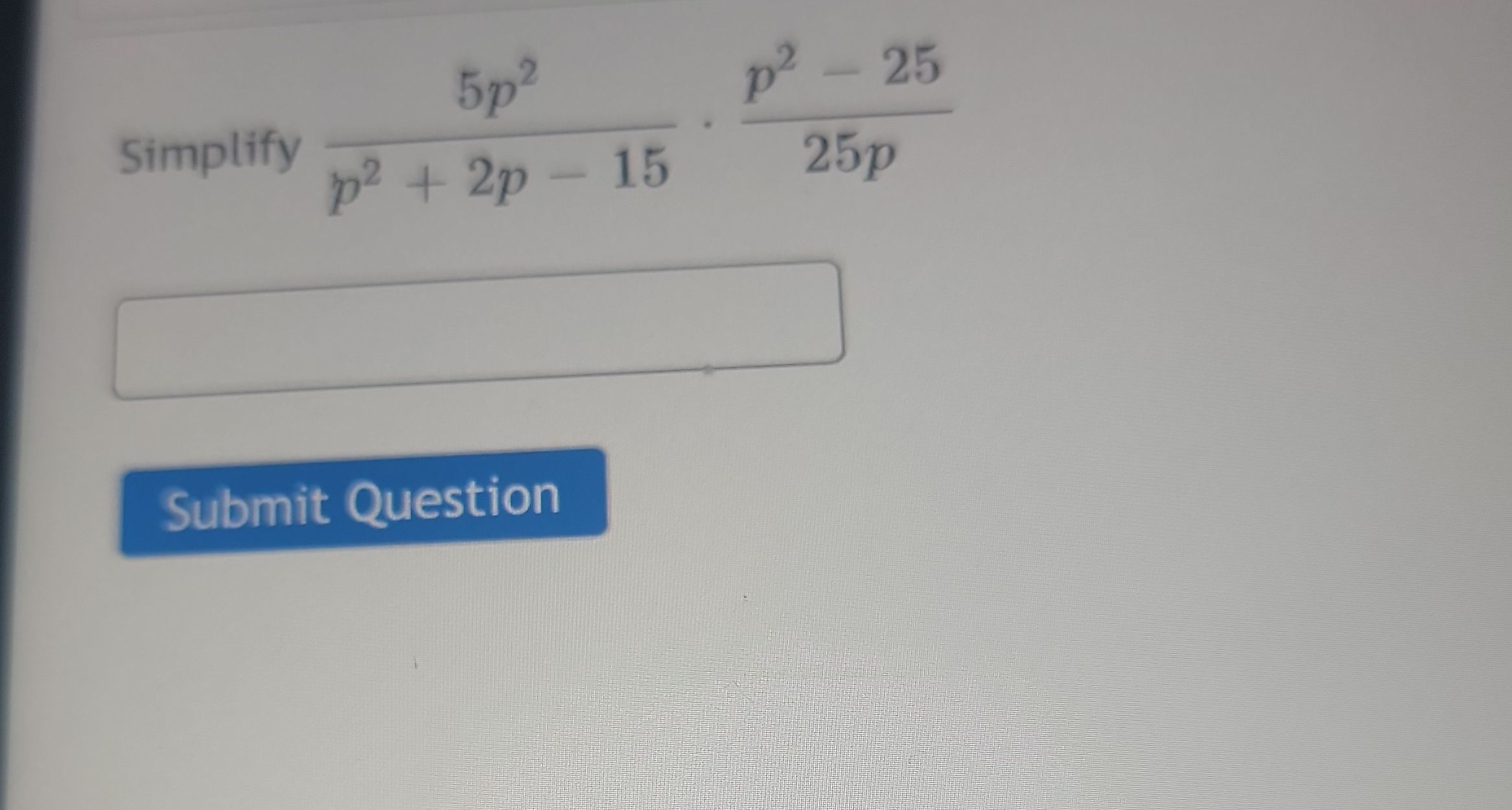
Simplify (5p^(2))/(p^(2)+2p-15)*(p^(2)-25)/(25 p)

Question

Simplify  (5p^(2))/(p^(2)+2p-15)*(p^(2)-25)/(25 p)

Bytelearn · Accepted Answer

Factor Quadratic Expressions: Factor the quadratic expressions where possible. The quadratic expression p^2 + 2p - 15 can be factored into (p + 5)(p - 3) because (p + 5)(p - 3) = p^2 - 3p + 5p - 15 = p^2 + 2p - 15. The quadratic expression p^2 - 25 can be factored into (p + 5)(p - 5) because (p + 5)(p - 5) = p^2 - 5p + 5p - 25 = p^2 - 25.Rewrite with Factored Forms: Rewrite the original expression with the factored forms. The expression becomes (5p^2)/((p + 5)(p - 3)) * ((p + 5)(p - 5))/(25p).Cancel Common Factors: Cancel out common factors. We can cancel out the common factor of (p + 5) from the numerator of the first fraction and the numerator of the second fraction. We can also cancel out p from 5p^2 in the numerator of the first fraction and 25p in the denominator of the second fraction. The expression now simplifies to (5p)/(p - 3) * (p - 5)/25.Simplify Further: Simplify the expression further. We can cancel out the common factor of 5 from 5p in the numerator and 25 in the denominator. The expression now simplifies to p/(p - 3) * (p - 5)/5.Multiply Remaining Expressions: Multiply the remaining expressions. Multiplying the numerators together and the denominators together, we get (p * (p - 5))/((p - 3) * 5).Expand Numerator: Expand the numerator. Expanding the numerator, we get p^2 - 5p. The expression now is (p^2 - 5p)/((p - 3) * 5).Leave Denominator Factored: Leave the denominator in factored form. The final simplified expression is (p^2 - 5p)/(5(p - 3)).

Simplify $\frac{5 p^{2}}{p^{2}+2 p-15} \cdot \frac{p^{2}-25}{25 p}$ $\newline$

Full solution

More problems from Divide numbers written in scientific notation

Related topics

Simplify 5p2p2+2p−15⋅p2−2525p \frac{5 p^{2}}{p^{2}+2 p-15} \cdot \frac{p^{2}-25}{25 p} p2+2p−155p2​⋅25pp2−25​\newline

Simplify $\frac{5 p^{2}}{p^{2}+2 p-15} \cdot \frac{p^{2}-25}{25 p}$ $\newline$