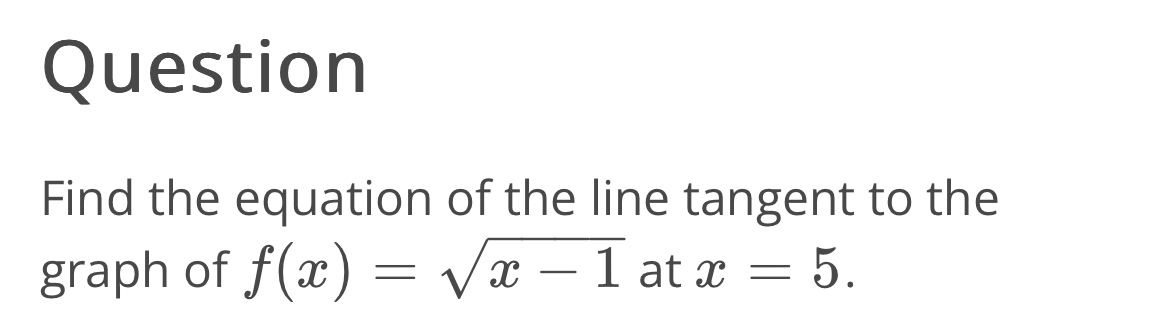Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Question
Find the equation of the line tangent to the graph of
f(x)=sqrt(x-1) at
x=5.

Question $\newline$ Find the equation of the line tangent to the graph of $f(x)=\sqrt{x-1}$ at $x=5$ .

View step-by-step help

View step-by-step help

Linear approximation

Full solution

Q. Question

\newline

Find the equation of the line tangent to the graph of

f(x)=\sqrt{x-1}

at

x=5

.

Find Derivative of $f(x)$ : First, we need to find the derivative of $f(x)$ to get the slope of the tangent line at $x = 5$ .
$f'(x) = (\frac{1}{2})(x - 1)^{-\frac{1}{2}} \cdot (1)$ by the chain rule.
Calculate Slope at x = $5$ : Now, plug in $x = 5$ into $f'(x)$ to find the slope at that point. $f'(5) = \left(\frac{1}{2}\right)(5 - 1)^{-\frac{1}{2}} = \left(\frac{1}{2}\right)(4)^{-\frac{1}{2}} = \left(\frac{1}{2}\right)\left(\frac{1}{2}\right) = \frac{1}{4}.$
Find y-coordinate at $x = 5$ : Next, find the y-coordinate of the point on the graph at $x = 5$ by plugging it into $f(x)$ . $f(5) = \sqrt{5 - 1} = \sqrt{4} = 2$ .
Write Equation of Tangent Line: Now we have a point $(5, 2)$ and a slope $\frac{1}{4}$ . Use the point-slope form to write the equation of the tangent line. $\newline$ $y - y_1 = m(x - x_1)$ , where $m$ is the slope and $(x_1, y_1)$ is the point. $\newline$ $y - 2 = \frac{1}{4}(x - 5)$ .
Simplify Equation to Slope-Intercept Form: Finally, simplify the equation to get it into slope-intercept form, $y = mx + b$ . $\newline$ $y = \frac{1}{4}x - \frac{1}{4}(5) + 2$ $\newline$ $y = \frac{1}{4}x - \frac{5}{4} + \frac{8}{4}$ $\newline$ $y = \frac{1}{4}x + \frac{3}{4}$ .

More problems from Linear approximation

Question

x^{2}+y^{2}=25

\newline

What is the value of

\frac{d^{2} y}{d x^{2}}

(4,3)

\newline

Give an exact number.

Posted 8 months ago

Question

For the function

f(x)=-10 x^{2}-10 x-8

, find the slope of the tangent line at

x=-10

\newline

Posted 9 months ago

Question

For the function

f(x)=8 x^{2}-2 x+11

, find the slope of the tangent line at

x=11

\newline

Posted 9 months ago

Question

For the following equation, evaluate

f^{\prime}(3)

\newline

f(x)=-5 x+1

\newline

Posted 9 months ago

Question

3

. Find the tangent line to

f(x)=

\left(2-4 x^{2}\right)^{5}

x=1

Posted 8 months ago

Question

f(x)=-x^{2}-12

f(4)

\newline

Posted 8 months ago

Question

f(x)=10(0.75)^x

x\geq0

is shown. What is the initial value of the function?

Posted 7 months ago

Question

\begin{cases} f(1)=37 \\\\ f(n)=f(n-1)\cdot 0.3 \end{cases}

\newline

Find an explicit formula for f(n).

Posted 7 months ago

Question

Solve for the exact value of

x

\newline

6 \ln (4 x+3)+19=37

\newline

Posted 8 months ago

Question

f

be an exponential function of the form

f(x)=a b^{x}

f(0)=4

f(3)=108

, what is the equation of

f

Posted 6 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant