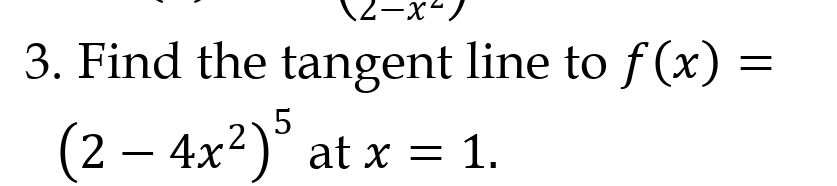Find the tangent line to f(x)= (2-4x^(2))^(5) at x=1

Question

Find the tangent line to  f(x)=  (2-4x^(2))^(5) at  x=1

Bytelearn · Accepted Answer

Find Derivative and Slope: To find the equation of the tangent line to the function at a specific point, we need to find the derivative of the function, which will give us the slope of the tangent line at any point x. We will then evaluate this derivative at x=1 to find the slope of the tangent line at that point.Apply Chain Rule: The function is f(x) = (2-4x^2)^5. We will use the chain rule to find its derivative. The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function.Calculate Derivative: Let's denote the inner function as g(x) = 2-4x^2 and the outer function as h(u) = u^5, where u = g(x). The derivative of h(u) with respect to u is h'(u) = 5u^4. The derivative of g(x) with respect to x is g'(x) = -8x.Evaluate at x=1: Now we apply the chain rule: f'(x) = h'(g(x)) * g'(x). Substituting the derivatives we found, we get f'(x) = 5(2-4x^2)^4 * (-8x).Find Point on Function: We evaluate the derivative at x=1: f'(1) = 5(2-4(1)^2)^4 * (-8(1)) = 5(2-4)^4 * (-8) = 5(-2)^4 * (-8) = 5*16*(-8) = -640.Use Point-Slope Form: The slope of the tangent line at x=1 is -640. Now we need the y-coordinate of the point on the function where x=1. We plug x=1 into the original function: f(1) = (2-4(1)^2)^5 = (2-4)^5 = (-2)^5 = -32.Substitute Values: We have the slope of the tangent line (-640) and a point on the tangent line (1, -32). The equation of a line is y = mx + b, where m is the slope and b is the y-intercept. We can use the point-slope form of the equation of a line to find the equation of the tangent line: y - y1 = m(x - x1), where (x1, y1) is the point on the line.Final Tangent Line Equation: Substituting the slope and the point into the point-slope form, we get y - (-32) = -640(x - 1). Simplifying, we get y + 32 = -640x + 640.Subtract 32 from both sides to get the final equation of the tangent line: y = -640x + 608.

$3$ . Find the tangent line to $f(x)=$ $\left(2-4 x^{2}\right)^{5}$ at $x=1$

Full solution

More problems from Linear approximation

Related topics

333. Find the tangent line to f(x)= f(x)= f(x)= (2−4x2)5 \left(2-4 x^{2}\right)^{5} (2−4x2)5 at x=1 x=1 x=1

$3$ . Find the tangent line to $f(x)=$ $\left(2-4 x^{2}\right)^{5}$ at $x=1$