Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

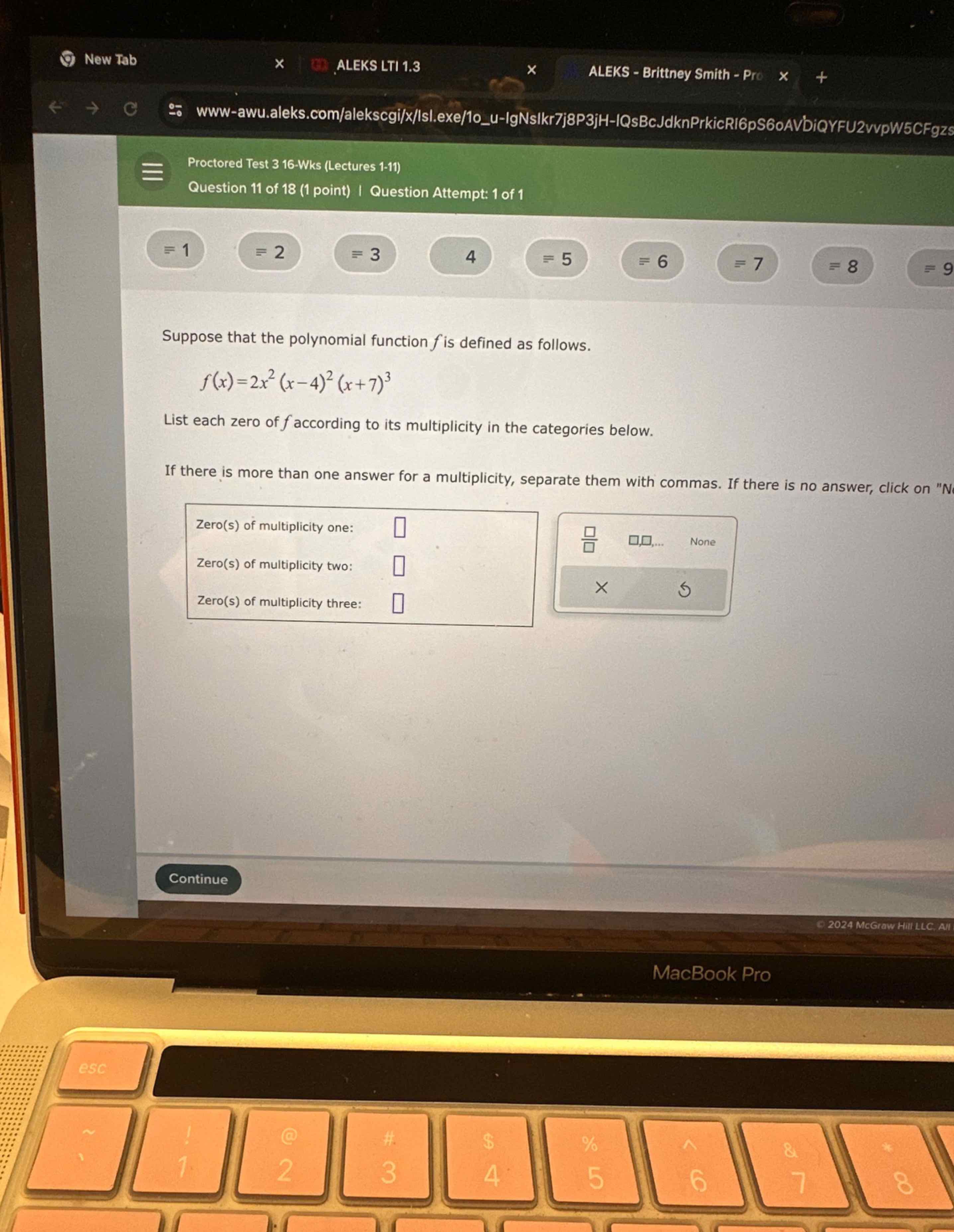
New Tab ALEKS LTI 1.3 ALEKS - Brittney Smith - Pre :'quad www-awu.aleks.com/alekscgi/X/Isl.exe/10_u-IgNsIkr7j8P3jH-IQsBcJdknPrkicRI6pS6oAVDiQYFU2vvpW5CFgzs Proctored Test 3 16-Wks (Lectures 1-11) Question 11 of 18 (1 point) I Question Attempt: 1 of 1 =1 -=2 -=3 4 =5 =6 =7 -=8 Suppose that the polynomial function f is defined as follows. f(x)=2x^(2)(x-4)^(2)(x+7)^(3) List each zero of f according to its multiplicity in the categories below. If there is more than one answer for a multiplicity, separate them with commas. If there is no answer, click on " N Zero(s) of multiplicity one: ◻ ◻ Zero(s) of multiplicity two: ◻ Zero(s) of multiplicity three: ◻ 믐 ㅁㅁ,... None x 6 Continue C. 2024 McGraw Hill LLC, All

Suppose that the polynomial function ff is defined as follows.\newlinef(x)=2x2(x−4)2(x+7)3f(x)=2x^{2}(x-4)^{2}(x+7)^{3}\newlineList each zero of ff according to its multiplicity in the categories below.\newlineIf there is more than one answer for a multiplicity, separate them with commas. If there is no answer, click on ＂N＂\newlineZero(s) of multiplicity one: \newline\newlineZero(s) of multiplicity two: \newline\newlineZero(s) of multiplicity three: \newline\newline

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Algebra 1right chevron icon
Transformations of functionsright chevron icon

Full solution

Q. Suppose that the polynomial function ff is defined as follows.\newlinef(x)=2x2(x−4)2(x+7)3f(x)=2x^{2}(x-4)^{2}(x+7)^{3}\newlineList each zero of ff according to its multiplicity in the categories below.\newlineIf there is more than one answer for a multiplicity, separate them with commas. If there is no answer, click on ＂N＂\newlineZero(s) of multiplicity one: \newline\newlineZero(s) of multiplicity two: \newline\newlineZero(s) of multiplicity three: \newline\newline
  1. Identify Zeros: Identify zeros from the polynomial f(x)=2x2(x−4)2(x+7)3f(x) = 2x^2(x-4)^2(x+7)^3.f(x)=0f(x) = 0 when x=0x = 0, x=4x = 4, or x=−7x = -7.
  2. Determine Multiplicity: Determine the multiplicity of each zero.\newlinex=0x = 0 appears in the term x2x^2, so its multiplicity is 22.\newlinex=4x = 4 appears in the term (x−4)2(x-4)^2, so its multiplicity is 22.\newlinex=−7x = -7 appears in the term (x+7)3(x+7)^3, so its multiplicity is 33.
  3. Categorize Zeros: Categorize zeros by their multiplicity.\newlineZero(s) of multiplicity one: None.\newlineZero(s) of multiplicity two: 00, 44.\newlineZero(s) of multiplicity three: −7-7.

More problems from Transformations of functions

Question
What does the transformation f(x)↦f(x)−6 f(x) \mapsto f(x) - 6 do to the graph of f(x) f(x) ?\newlineChoices:\newline(A) translates it 6 units down\text{translates it } 6 \text{ units down}\newline(B) translates it 6 units right\text{translates it } 6 \text{ units right}\newline(C) translates it 6 units left\text{translates it } 6 \text{ units left}\newline(D) translates it 6 units up\text{translates it } 6 \text{ units up}
Get tutor helpright-arrow

Posted 5 months ago

Question
Find g(x)g(x), where g(x)g(x) is the reflection across the yy-axis of f(x)=−4x+1f(x) = -4x + 1.\newlineChoices:\newline[g(x) = 4x - 1]\text{[g(x) = 4x - 1]}\newline[g(x) = -4x + 1]\text{[g(x) = -4x + 1]}\newline[g(x) = 4x + 1]\text{[g(x) = 4x + 1]}\newline[g(x) = -4x - 1]\text{[g(x) = -4x - 1]}
Get tutor helpright-arrow

Posted 5 months ago

Question
What kind of transformation converts the graph of f(x)=−8(x−4)2+6 f(x) = -8(x - 4)^2 + 6 into the graph of g(x)=−8(x+6)2+6 g(x) = -8(x + 6)^2 + 6 ?\newlineChoices:\newline[A]translation 10 units left\text{[A]translation 10 units left}\newline[B]translation 10 units right\text{[B]translation 10 units right}\newline[C]translation 10 units up\text{[C]translation 10 units up}\newline[D]translation 10 units down\text{[D]translation 10 units down}
Get tutor helpright-arrow

Posted 5 months ago

Question
Find g(x)g(x), where g(x)g(x) is the reflection across the x-axis of f(x)=−6(x−7)2+2f(x) = -6(x - 7)^2 + 2.\newlineChoices:\newline(A) g(x)=6(x−7)2−2g(x) = 6(x - 7)^2 - 2\newline(B) g(x)=−6(x+7)2+2g(x) = -6(x + 7)^2 + 2\newline(C) g(x)=−6(x−7)2−2g(x) = -6(x - 7)^2 - 2\newline(D) g(x)=6(x+7)2−2g(x) = 6(x + 7)^2 - 2
Get tutor helpright-arrow

Posted 5 months ago

Question
lim⁡x→π4cos⁡(x)=? \lim _{x \rightarrow \frac{\pi}{4}} \cos (x)=? \newlineChoose 11 answer:\newline(A) 12 \frac{1}{2} \newline(B) 11\newline(C) 22 \frac{\sqrt{2}}{2} \newline(D) The limit doesn't exist.
Get tutor helpright-arrow

Posted 10 months ago

Question
Tess tried to solve the differential equation dydx=2xy−6x \frac{d y}{d x}=2 x y-6 x . This is her work:\newlinedydx=2xy−6x \frac{d y}{d x}=2 x y-6 x \newlineStep 11: dydx=(y−3)2x\quad \frac{d y}{d x}=(y-3) 2 x \newlineStep 22: ∫1y−3dy=∫2xdx \quad \int \frac{1}{y-3} d y=\int 2 x d x \newlineStep 33: ln⁡∣y−3∣=x2+C1 \quad \ln |y-3|=x^{2}+C_{1} \newlineStep 44: eln⁡∣y−3∣=ex2+C1 \quad e^{\ln |y-3|}=e^{x^{2}}+C_{1} \newlineStep 55: ∣y−3∣=ex2+C1 \quad|y-3|=e^{x^{2}}+C_{1} \newlineStep 66: y−3=±ex2+C2 \quad y-3= \pm e^{x^{2}}+C_{2} \newlineStep 77: y=±ex2+C \quad y= \pm e^{x^{2}}+C \newlineIs Tess's work correct? If not, what is her mistake?\newlineChoose 11 answer:\newline(A) Tess's work is correct.\newline(B) Step 11 is incorrect. We're not allowed to factor an expression when solving differential equations.\newline(C) Step 44 is incorrect. The right-hand side of the equation should be ex2+C1 e^{x^{2}+C_{1}} .\newline(D) Step 77 is incorrect. Tess didn't account for adding 33 to the right side.
Get tutor helpright-arrow

Posted 8 months ago

Question
Aditya tried to solve the differential equation dydx=6x−30 \frac{d y}{d x}=6 x-30 . This is his work:\newlinedydx=6x−30 \frac{d y}{d x}=6 x-30 \newlineStep 11: ∫30dy=∫6xdx \quad \int 30 d y=\int 6 x d x \newlineStep 22: 30y=3x2+C \quad 30 y=3 x^{2}+C \newlineStep 33: y=x210+C \quad y=\frac{x^{2}}{10}+C \newlineIs Aditya's work correct? If not, what is his mistake?\newlineChoose 11 answer:\newline(A) Aditya's work is correct.\newline(B) Step 11 is incorrect. The separation of variables wasn't done correctly.\newline(C) Step 22 is incorrect. Aditya didn't integrate 3030 correctly.\newline(D) Step 33 is incorrect. The right-hand side of the equation should be 303x2+C \frac{30}{3 x^{2}+C} .
Get tutor helpright-arrow

Posted 9 months ago

Question
Jonael dropped a sandbag from a hot air balloon at a target that is 250250 meters below the balloon. At this moment, the sandbag is 7575 meters below the balloon.\newlineWhich 22 of the following expressions represents the distance between the sandbag and the target?\newlineChoose 22 answers:\newline(A) ∣−250+75∣|-250+75|\newline(B) ∣250+75∣|250+75|\newline(C) ∣−75+250∣|-75+250|
Get tutor helpright-arrow

Posted 9 months ago

Question
f(x)=−(x+1)(x+7)f(x) = -(x+1)(x+7)\newlineThe function represents a parabola in the xyxy-plane. Which of the following is an equivalent form of ff in which the yy-intercept of the graph of ff appears as a constant or coefficient?\newlineChoose 11 answer:\newline(A) f(x)=−(x+4)2+9f(x) = -(x+4)^{2}+9\newline(B) f(x)=−(x+4)2−9f(x) = -(x+4)^{2}-9\newline(C) f(x)=−x2+8x+7f(x) = -x^{2}+8x+7\newline(D) f(x)=−x2−8x−7f(x) = -x^{2}-8x-7
Get tutor helpright-arrow

Posted 9 months ago

Question
Determine whether the function f(x) f(x) is continuous at x=−3 x=-3 .\newlinef(x)={18−x2,x≤−315+3x,x>−3 f(x)=\left\{\begin{array}{ll} 18-x^{2}, & x \leq-3 \\ 15+3 x, & x>-3 \end{array}\right. \newlinef(x) f(x) is discontinuous at x=−3 x=-3 \newlinef(x) f(x) is continuous at x=−3 x=-3
Get tutor helpright-arrow

Posted 9 months ago

View all (26)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant