AI tutor
Full solution
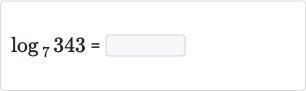
Q.
- Problem Understanding: Understand the problem.We need to find the exponent to which the base must be raised to get the number .
- Expressing as a Power of : Express as a power of . is raised to the power of , since .
- Applying the Definition of Logarithm: Apply the definition of logarithm.If , then .Since we know that is , we can say that .
- Concluding the Solution: Conclude the solution.Therefore, .
More problems from Powers of i
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help