Full solution
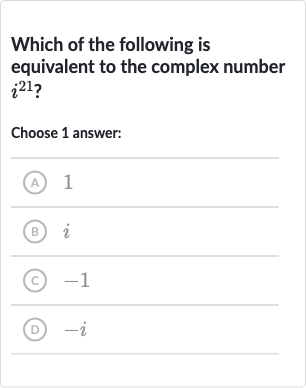
Q. Which of the following is equivalent to the complex number ?Choose answer:(A) (B) (C) (D)
- Determine pattern of powers: Determine the pattern of powers of .The powers of follow a cyclical pattern:Then the pattern repeats every powers.
- Reduce exponent modulo : Reduce the exponent modulo to find its equivalent in the pattern.This means that is equivalent to in the pattern.
- Match reduced exponent to pattern: Match the reduced exponent to the pattern.Since , we look at the pattern and see that .
More problems from Powers of i
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help