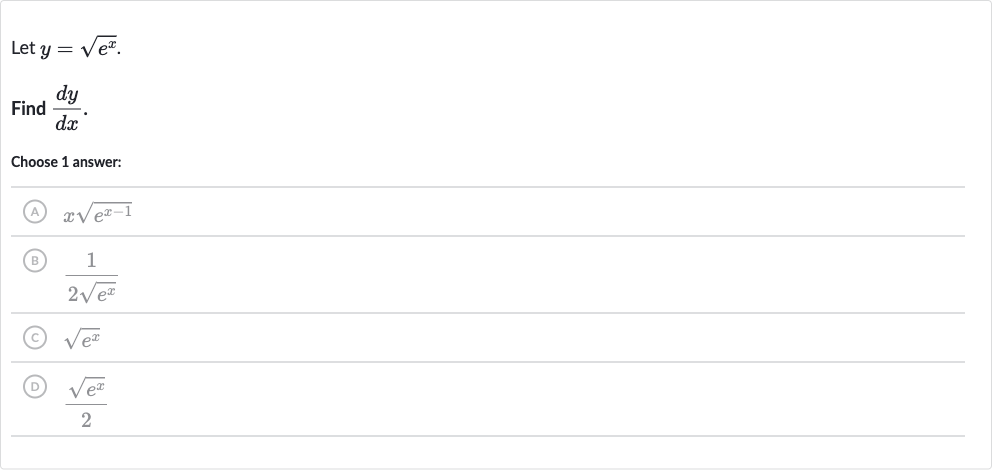
Let y=sqrt(e^(x)). Find (dy)/(dx). Choose 1 answer: (A) xsqrt(e^(x-1)) (B) (1)/(2sqrt(e^(x))) (C) sqrt(e^(x)) (D) (sqrt(e^(x)))/(2)

Question

Let  y=sqrt(e^(x)). Find  (dy)/(dx). Choose 1 answer: (A)  xsqrt(e^(x-1)) (B)  (1)/(2sqrt(e^(x))) (C)  sqrt(e^(x)) (D)  (sqrt(e^(x)))/(2)

Bytelearn · Accepted Answer

Write Function, Variable: Write down the function and identify the differentiation variable. We have the function y = sqrt(e^x). We want to find the derivative of y with respect to x, which is denoted as (dy)/(dx).Apply Chain Rule: Apply the chain rule for differentiation. The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. In this case, the outer function is the square root function, and the inner function is e^x.Differentiate Outer Function: Differentiate the outer function with respect to the inner function. The derivative of sqrt(u) with respect to u is (1)/(2sqrt(u)), where u is the inner function. In this case, u = e^x, so the derivative of the outer function is (1)/(2sqrt(e^x)).Differentiate Inner Function: Differentiate the inner function with respect to x. The derivative of e^x with respect to x is e^x. So, the derivative of the inner function is e^x.Multiply Derivatives: Multiply the derivatives of the outer and inner functions. Using the chain rule from Step 2, we multiply the derivative of the outer function from Step 3 by the derivative of the inner function from Step 4. This gives us (dy)/(dx) = (1)/(2sqrt(e^x)) * e^x.Simplify Expression: Simplify the expression. We can simplify the expression by canceling out one e^x in the numerator with the e^x in the denominator of the square root. This leaves us with (dy)/(dx) = (e^x)/(2sqrt(e^x)).Recognize Simplification: Recognize that e^x/sqrt(e^x) is the same as sqrt(e^x). Since e^x is the same as (sqrt(e^x))^2, we can simplify the expression further to get (dy)/(dx) = (sqrt(e^x))/(2).

Let $y=\sqrt{e^{x}}$ . $\newline$ Find $\frac{d y}{d x}$ . $\newline$ Choose $1$ answer: $\newline$ (A) $x \sqrt{e^{x-1}}$ $\newline$ (B) $\frac{1}{2 \sqrt{e^{x}}}$ $\newline$ (C) $\sqrt{e^{x}}$ $\newline$ (D) $\frac{\sqrt{e^{x}}}{2}$

Full solution

More problems from Domain and range of square root functions: equations

Related topics

Let y=ex y=\sqrt{e^{x}} y=ex​.\newlineFind dydx \frac{d y}{d x} dxdy​.\newlineChoose 111 answer:\newline(A) xex−1 x \sqrt{e^{x-1}} xex−1​\newline(B) 12ex \frac{1}{2 \sqrt{e^{x}}} 2ex​1​\newline(C) ex \sqrt{e^{x}} ex​\newline(D) ex2 \frac{\sqrt{e^{x}}}{2} 2ex​​

Let $y=\sqrt{e^{x}}$ . $\newline$ Find $\frac{d y}{d x}$ . $\newline$ Choose $1$ answer: $\newline$ (A) $x \sqrt{e^{x-1}}$ $\newline$ (B) $\frac{1}{2 \sqrt{e^{x}}}$ $\newline$ (C) $\sqrt{e^{x}}$ $\newline$ (D) $\frac{\sqrt{e^{x}}}{2}$