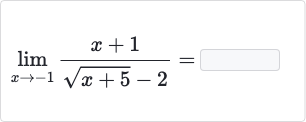lim_(x rarr-1)(x+1)/(sqrt(x+5)-2)=

Question

Bytelearn · Accepted Answer

Identify Function and Point: Identify the function and the point at which we need to find the limit. We have the function f(x) = (x+1)/(sqrt(x+5)-2) and we need to find the limit as x approaches -1.Direct Substitution: Direct substitution to check if the limit can be found this way. Let's substitute x = -1 into the function to see if we get a determinate form. f(-1) = (-1+1)/(sqrt(-1+5)-2) = 0/(sqrt(4)-2) = 0/0, which is an indeterminate form.Manipulate Function: Since we have an indeterminate form, we need to manipulate the function to find the limit. We can use the conjugate of the denominator to rationalize the expression. The conjugate of sqrt(x+5)-2 is sqrt(x+5)+2.Multiply by Conjugate: Multiply the numerator and the denominator by the conjugate of the denominator. f(x) = [(x+1)(sqrt(x+5)+2)] / [(sqrt(x+5)-2)(sqrt(x+5)+2)]Simplify Expression: Simplify the expression by using the difference of squares formula (a-b)(a+b) = a^2 - b^2. f(x) = [(x+1)(sqrt(x+5)+2)] / [(x+5) - (2^2)] f(x) = [(x+1)(sqrt(x+5)+2)] / [x+5 - 4] f(x) = [(x+1)(sqrt(x+5)+2)] / [x+1]Cancel Common Factor: Cancel out the common factor of (x+1) in the numerator and the denominator. f(x) = (sqrt(x+5)+2)Substitute to Find Limit: Now that we have simplified the function, let's substitute x = -1 again to find the limit. lim_(x -> -1) f(x) = sqrt(-1+5)+2 = sqrt(4)+2 = 2+2 = 4

$\lim _{x \rightarrow-1} \frac{x+1}{\sqrt{x+5}-2}=$

Full solution

More problems from Domain and range of square root functions: equations

Related topics

lim⁡x→−1x+1x+5−2= \lim _{x \rightarrow-1} \frac{x+1}{\sqrt{x+5}-2}= limx→−1​x+5​−2x+1​=

$\lim _{x \rightarrow-1} \frac{x+1}{\sqrt{x+5}-2}=$