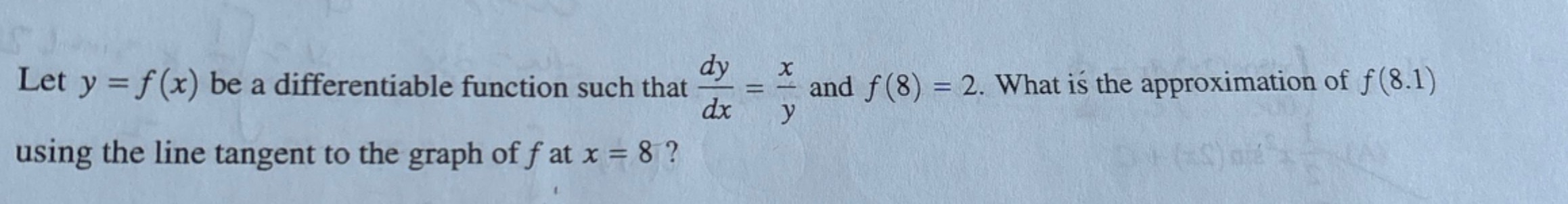Full solution
Q. Let be a differentiable function such that and . What is the approximation of using the line tangent to the graph of at ?
- Identify derivative & point: Identify the derivative and the point of interest.Given that and , we need to find the derivative at .
- Calculate derivative at : Calculate the derivative at . at is .
- Use point-slope form: Use the point-slope form of the equation of a line to find the tangent line.The slope of the tangent line at is , and the point on the curve is .Equation of the tangent line: .
- Simplify tangent line equation: Simplify the equation of the tangent line. ,.
- Approximate : Use the tangent line to approximate .Substitute into the tangent line equation:,,.