AI tutor
Full solution
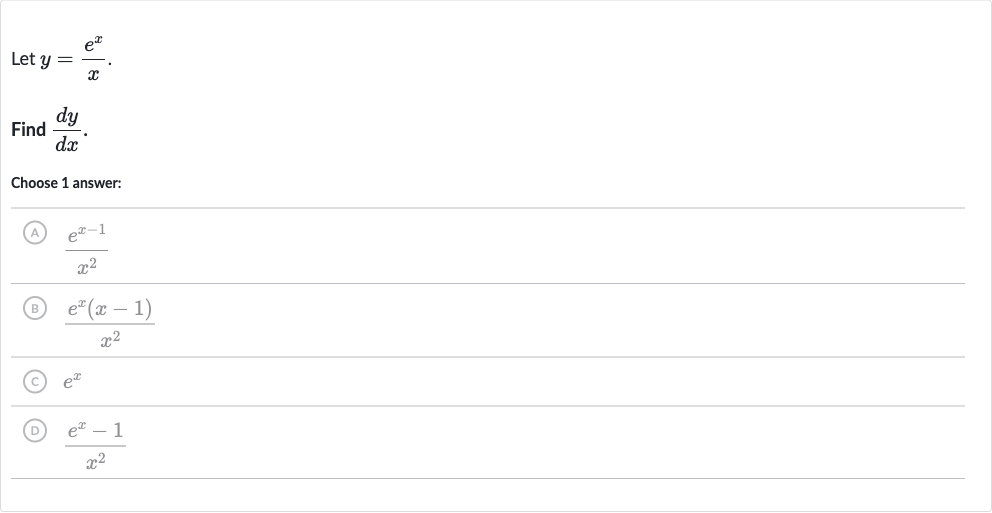
Q. Let .Find .Choose answer:(A) (B) (C) (D)
- Identify function: Identify the function to differentiate.We are given the function , and we need to find its derivative with respect to . This is a quotient of two functions, so we will use the quotient rule for differentiation.
- Apply quotient rule: Apply the quotient rule.The quotient rule states that the derivative of a function is given by . Here, and .
- Differentiate functions: Differentiate and . The derivative of with respect to is . The derivative of with respect to is .
- Plug derivatives into formula: Plug the derivatives into the quotient rule formula. Using the derivatives from Step , we get .
- Simplify expression: Simplify the expression.Simplify the numerator: .Now the derivative is .
- Match with options: Match the result with the given options.The simplified derivative matches option .