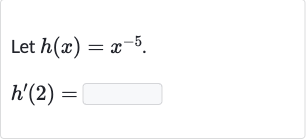AI tutor
Full solution
Q. Let .
- Identify Function & Point: Identify the function and the point at which we need to find the derivative. The function given is , and we need to find the derivative of at , denoted as .
- Differentiate with Respect: Differentiate the function with respect to . The derivative of with respect to is . Therefore, the derivative of is .
- Substitute : Substitute into the derivative to find ..
- Calculate : Calculate the value of ., so .
More problems from Write and solve inverse variation equations
QuestionGet tutor help