AI tutor
Full solution
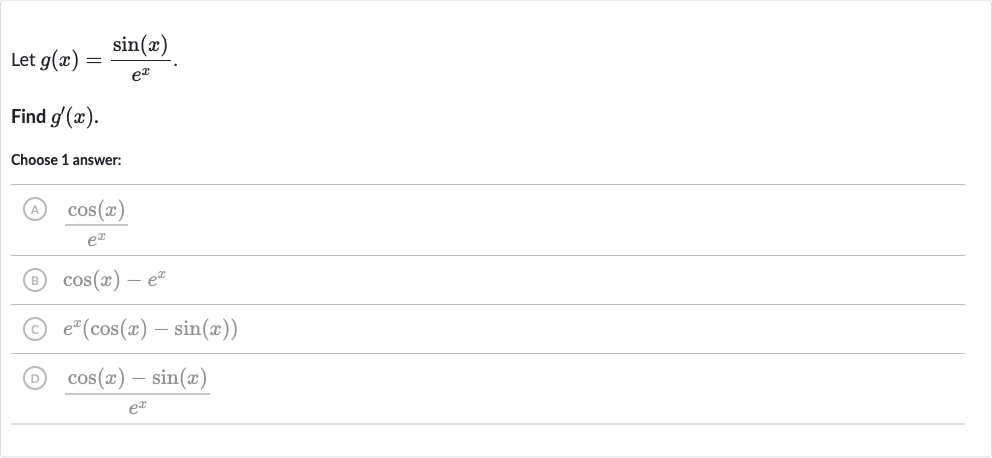
Q. Let .Find .Choose answer:(A) (B) (C) (D)
- Apply Quotient Rule: Apply the quotient rule to find the derivative of . The quotient rule states that if you have a function , then .
- Identify Functions: Identify the functions and where and . We need to find the derivatives and .
- Find : Find the derivative of . The derivative of with respect to is , so .
- Find : Find the derivative of . The derivative of with respect to is , so .
- Apply Quotient Rule: Apply the quotient rule using the derivatives from steps and . .
- Simplify Expression: Simplify the expression from step . Since is common in both terms in the numerator, we can factor it out.
- Match Correct Answer: Simplify further by canceling out one from the numerator and denominator. .
- Match Correct Answer: Simplify further by canceling out one from the numerator and denominator. .Match the simplified derivative to the given answer choices. The correct answer is (D) .