AI tutor
Full solution
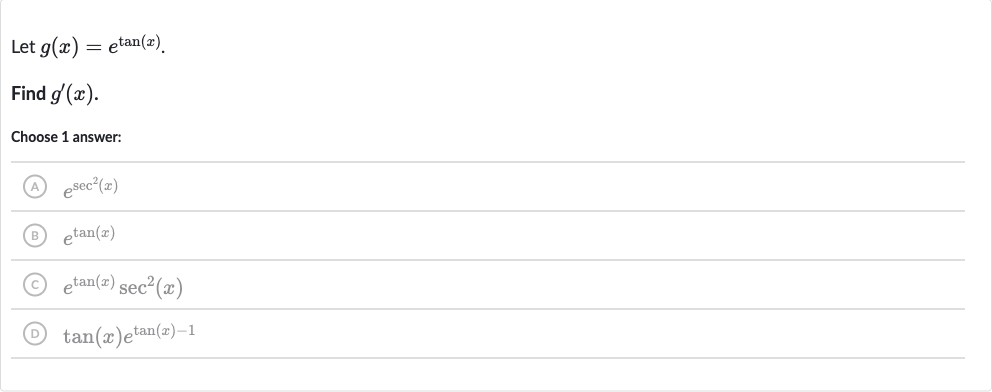
Q. Let .Find .Choose answer:(A) (B) (C) (D)
- Identify Functions: We need to find the derivative of the function . To do this, we will use the chain rule, which states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function.
- Derivative of Outer Function: First, let's identify the outer and inner functions. The outer function is , where is the inner function. The inner function is .
- Derivative of Inner Function: Now, we take the derivative of the outer function with respect to the inner function. The derivative of with respect to is .
- Apply Chain Rule: Next, we take the derivative of the inner function with respect to . The derivative of is .
- Match with Options: Applying the chain rule, we multiply the derivative of the outer function by the derivative of the inner function.
- Match with Options: Applying the chain rule, we multiply the derivative of the outer function by the derivative of the inner function.We can now match our result with the given options. The correct answer is:This corresponds to option (C).