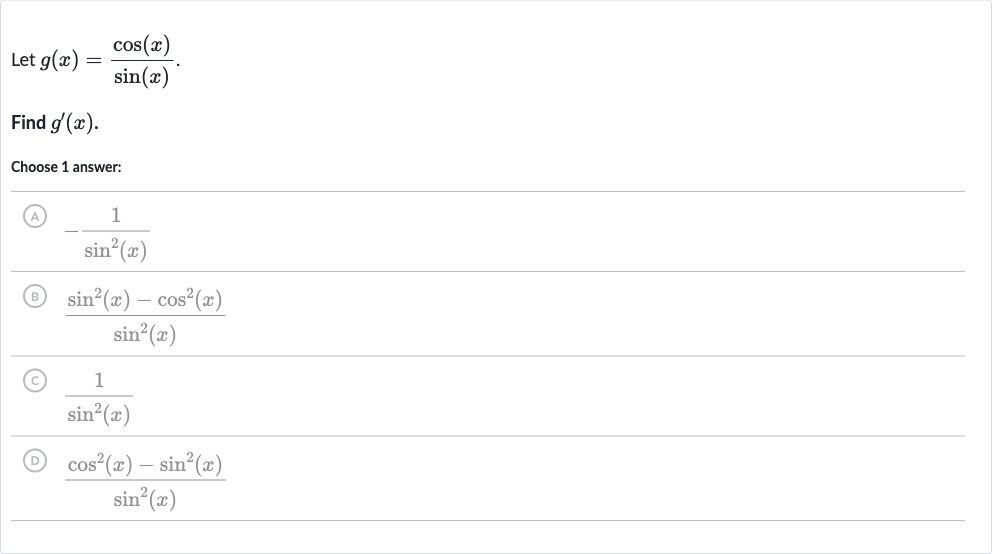
Let g(x)=(cos(x))/(sin(x)). Find g^(')(x). Choose 1 answer: (A) -(1)/(sin^(2)(x)) (B) (sin^(2)(x)-cos^(2)(x))/(sin^(2)(x)) (C) (1)/(sin^(2)(x)) (D) (cos^(2)(x)-sin^(2)(x))/(sin^(2)(x))

Question

Let  g(x)=(cos(x))/(sin(x)). Find  g^(')(x). Choose 1 answer: (A)  -(1)/(sin^(2)(x)) (B)  (sin^(2)(x)-cos^(2)(x))/(sin^(2)(x)) (C)  (1)/(sin^(2)(x)) (D)  (cos^(2)(x)-sin^(2)(x))/(sin^(2)(x))

Bytelearn · Accepted Answer

Recognize Function Type: Recognize that g(x) = (cos(x))/(sin(x)) is a quotient of two functions, where the numerator is cos(x) and the denominator is sin(x). To find the derivative g'(x), we will use the quotient rule.Apply Quotient Rule: The quotient rule states that if we have a function h(x) = f(x)/g(x), then its derivative h'(x) is given by h'(x) = (f'(x)g(x) - f(x)g'(x))/(g(x))^2. Here, f(x) = cos(x) and g(x) = sin(x).Find Derivative of Cos(x): Find the derivative of the numerator f(x) = cos(x). The derivative of cos(x) with respect to x is -sin(x).Find Derivative of Sin(x): Find the derivative of the denominator g(x) = sin(x). The derivative of sin(x) with respect to x is cos(x).Apply Quotient Rule: Apply the quotient rule using the derivatives from steps 3 and 4. So, g'(x) = (-sin(x) * sin(x) - cos(x) * cos(x)) / (sin(x))^2.Simplify Expression: Simplify the expression for g'(x). We have g'(x) = (-sin^2(x) - cos^2(x)) / sin^2(x).Apply Pythagorean Identity: Recognize that sin^2(x) + cos^2(x) = 1, which is the Pythagorean identity. Therefore, -sin^2(x) - cos^2(x) = -1.Substitute Identity: Substitute the Pythagorean identity into the expression for g'(x) to get g'(x) = -1 / sin^2(x).Final Simplified Form: The final simplified form of g'(x) is g'(x) = -(1) / sin^2(x), which corresponds to answer choice (A).

Full solution

More problems from Find derivatives of using multiple formulae

Related topics