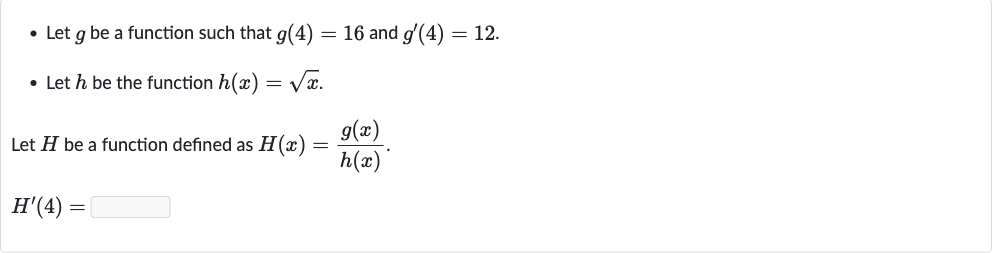Full solution
Q. - Let be a function such that and .- Let be the function .Let be a function defined as .
- Write function: First, let's write down the function using the given functions and : .
- Find derivative : Now, we need to find the derivative of , which is . We'll use the quotient rule for derivatives, which is , where is the numerator and is the denominator.
- Derivatives of and : Let's find the derivatives of and . We know . For , the derivative is . So .
- Apply quotient rule: Now we apply the quotient rule. .
- Plug in : Let's plug in the values for . .
- Substitute known values: Substitute the known values: .
- Calculate values: Calculate the values:
- Simplify expression: Simplify the expression:
- Finish calculation: Finish the calculation:
- Final result: So, .