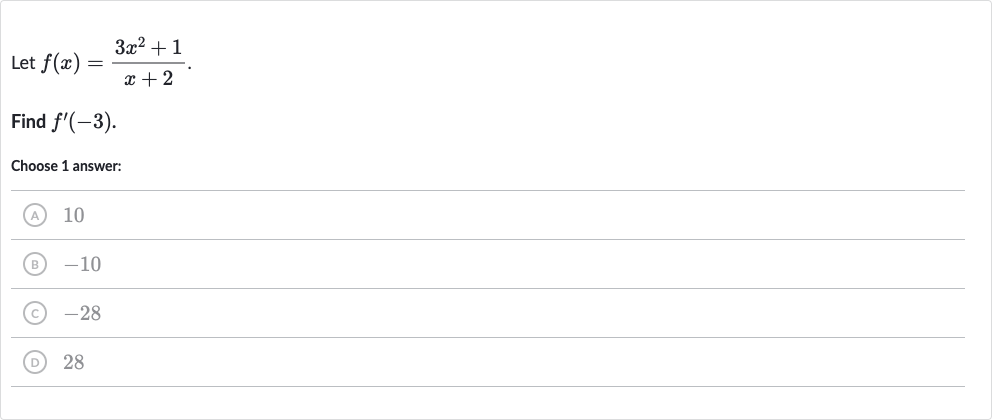
Let f(x)=(3x^(2)+1)/(x+2). Find f^(')(-3). Choose 1 answer: (A) 10 (B) -10 (C) -28 (D) 28

Question

Let  f(x)=(3x^(2)+1)/(x+2). Find  f^(')(-3). Choose 1 answer: (A)  10 (B) -10 (C) -28 (D) 28

Bytelearn · Accepted Answer

Apply Quotient Rule: To find the derivative of the function f(x) = (3x^2 + 1) / (x + 2), we will use the quotient rule. The quotient rule states that if we have a function that is the quotient of two functions, u(x) / v(x), then its derivative is given by (v(x) * u'(x) - u(x) * v'(x)) / (v(x))^2. Here, u(x) = 3x^2 + 1 and v(x) = x + 2.Find u'(x): First, we need to find the derivative of u(x) = 3x^2 + 1. The derivative of 3x^2 is 6x, and the derivative of a constant is 0. Therefore, u'(x) = 6x.Find v'(x): Next, we need to find the derivative of v(x) = x + 2. The derivative of x is 1, and the derivative of a constant is 0. Therefore, v'(x) = 1.Apply Quotient Rule: Now we apply the quotient rule. The derivative of f(x), denoted as f'(x), is given by: f'(x) = ((x + 2) * (6x) - (3x^2 + 1) * (1)) / (x + 2)^2.Simplify f'(x): We simplify the expression for f'(x): f'(x) = (6x^2 + 12x - 3x^2 - 1) / (x + 2)^2.Combine Like Terms: Further simplifying, we combine like terms in the numerator: f'(x) = (3x^2 + 12x - 1) / (x + 2)^2.Evaluate at x = -3: Now we need to evaluate f'(x) at x = -3. We substitute -3 into the derivative: f'(-3) = (3(-3)^2 + 12(-3) - 1) / ((-3) + 2)^2.Calculate Numerator and Denominator: We calculate the numerator and the denominator separately: Numerator: 3(-3)^2 + 12(-3) - 1 = 3(9) - 36 - 1 = 27 - 36 - 1 = -10. Denominator: ((-3) + 2)^2 = (-1)^2 = 1.Divide Numerator by Denominator: Now we divide the numerator by the denominator: f'(-3) = (-10) / 1 = -10.

Let $f(x)=\frac{3 x^{2}+1}{x+2}$ . $\newline$ Find $f^{\prime}(-3)$ . $\newline$ Choose $1$ answer: $\newline$ (A) $\mathbf{1 0}$ $\newline$ (B) $-10$ $\newline$ (C) $-28$ $\newline$ (D) $28$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Let f(x)=3x2+1x+2 f(x)=\frac{3 x^{2}+1}{x+2} f(x)=x+23x2+1​.\newlineFind f′(−3) f^{\prime}(-3) f′(−3).\newlineChoose 111 answer:\newline(A) 10 \mathbf{1 0} 10\newline(B) −10-10−10\newline(C) −28-28−28\newline(D) 282828

Let $f(x)=\frac{3 x^{2}+1}{x+2}$ . $\newline$ Find $f^{\prime}(-3)$ . $\newline$ Choose $1$ answer: $\newline$ (A) $\mathbf{1 0}$ $\newline$ (B) $-10$ $\newline$ (C) $-28$ $\newline$ (D) $28$