AI tutor
Full solution
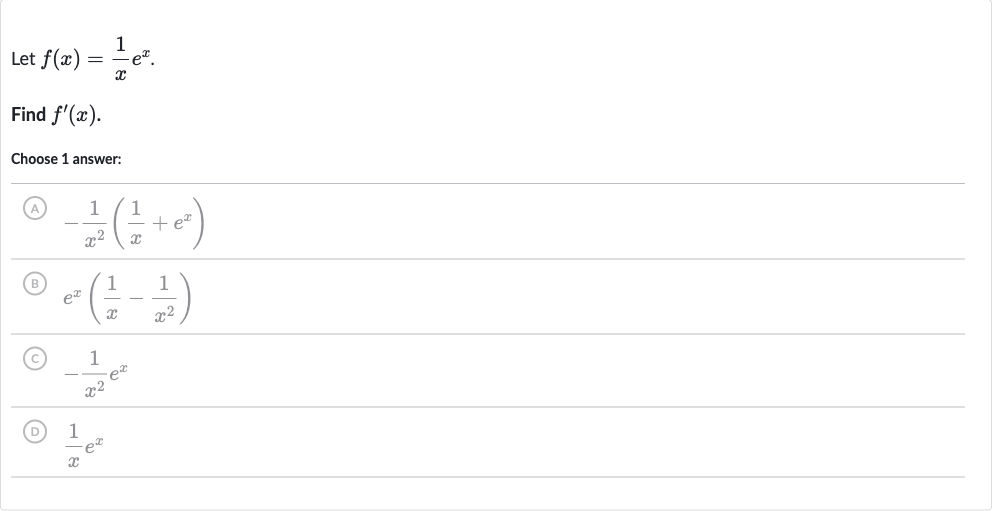
Q. Let .Find .Choose answer:(A) (B) (C) (D)
- Use product rule: Use the product rule for derivatives: .
- Find and : Let and . Now find the derivatives and .
- Apply product rule: The derivative of is .
- Substitute into formula: The derivative of is .
- Simplify expression: Now apply the product rule: .
- Combine terms: Substitute , , , and into the formula: .
- Factor out : Simplify the expression: .
- Factor out : Simplify the expression: .Combine the terms: .
- Factor out : Simplify the expression: .Combine the terms: .Factor out : .