Full solution
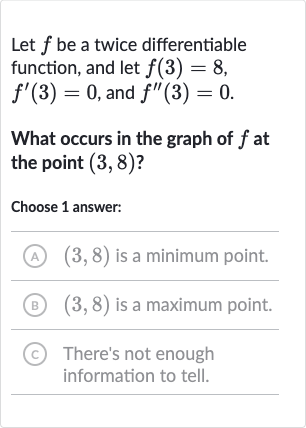
Q. Let be a twice differentiable function, and let , , and .What occurs in the graph of at the point ?Choose answer:(A) is a minimum point.(B) is a maximum point.(C) There's not enough information to tell.
- Given Information: To determine what occurs at the point , we need to analyze the given information about the function and its derivatives at .Given:, which means the point lies on the graph of ., which indicates that the slope of the tangent to the graph of at is zero. This could mean that is a maximum, a minimum, or a point of inflection., which means the concavity of the graph at is neither upwards nor downwards. This does not provide conclusive information about whether is a maximum or minimum point.
- Analysis of : To determine if is a maximum or minimum point, we would need the sign of the second derivative around . Since , we cannot conclude whether the graph is concave up or concave down at this point. If were positive for near , it would indicate a minimum point. If were negative for near , it would indicate a maximum point. However, with , we cannot make this determination.
- Determining Maximum or Minimum: Since we do not have information about the behavior of around other than at the exact point , we cannot determine if is a maximum or minimum point. We need additional information about the concavity of near to make a definitive conclusion.
More problems from One-step inequalities: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help