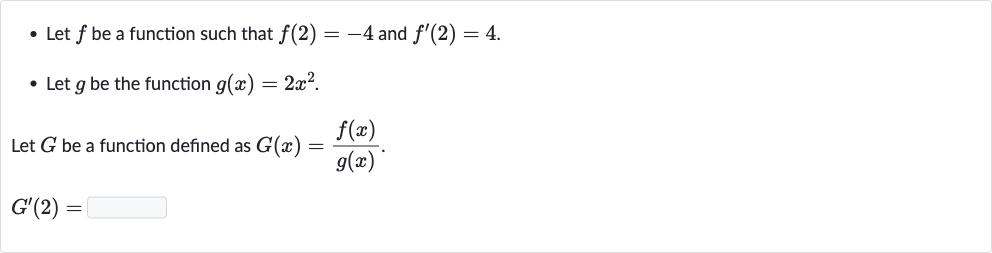Let f be a function such that f(2)=-4 and f^(')(2)=4. Let g be the function g(x)=2x^(2). Let G be a function defined as G(x)=(f(x))/(g(x)). G^(')(2)=

Question

Let  f be a function such that  f(2)=-4 and  f^(')(2)=4. Let  g be the function  g(x)=2x^(2).  Let  G be a function defined as  G(x)=(f(x))/(g(x)).  G^(')(2)=

Bytelearn · Accepted Answer

Given values: We are given that f(2) = -4 and f'(2) = 4. We also know that g(x) = 2x^2. To find G'(2), we need to use the quotient rule for derivatives, which states that if h(x) = u(x)/v(x), then h'(x) = (u'(x)v(x) - u(x)v'(x))/(v(x))^2. Here, u(x) = f(x) and v(x) = g(x).Find g'(x): First, we need to find g'(x). Since g(x) = 2x^2, we can differentiate it with respect to x to get g'(x) = 4x.Evaluate g'(2): Now we can evaluate g'(2). Substituting x = 2 into g'(x) = 4x, we get g'(2) = 4 * 2 = 8.Apply quotient rule: Next, we apply the quotient rule using the values we have: G'(x) = (f'(x)g(x) - f(x)g'(x)) / (g(x))^2. We substitute x = 2 into the equation to find G'(2): G'(2) = (f'(2)g(2) - f(2)g'(2)) / (g(2))^2.Find g(2): We already know that f(2) = -4, f'(2) = 4, and g'(2) = 8. Now we need to find g(2). Substituting x = 2 into g(x) = 2x^2, we get g(2) = 2 * 2^2 = 2 * 4 = 8.Calculate G'(2): Now we have all the values we need to calculate G'(2): G'(2) = (4 * 8 - (-4) * 8) / (8)^2.Simplify numerator: Simplify the numerator: G'(2) = (32 + 32) / 64.Simplify fraction: Simplify the fraction: G'(2) = 64 / 64.Final result: G'(2) = 1.

- Let $f$ be a function such that $f(2)=-4$ and $f^{\prime}(2)=4$ . $\newline$ - Let $g$ be the function $g(x)=2 x^{2}$ . $\newline$ Let $G$ be a function defined as $G(x)=\frac{f(x)}{g(x)}$ . $\newline$ $G^{\prime}(2)=$

Full solution

More problems from Write variable expressions for arithmetic sequences

Related topics